Le champ de force central a été traité avec le formalisme vectoriel de Newton et le théorème du moment cinétique dans le chapitre " Problèmes à 2 corps" du grain précédent.
Il s'agit ici du traitement général du problème à deux corps soumis à une force centrale réciproque, par le formalisme lagrangien.
Dans ce chapitre seront exploitées les lois de conservation pour effectuer la réduction canonique du problème à deux corps (
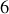 degrés de liberté) à un problème à un corps (
degrés de liberté) à un problème à un corps (
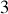 ).
).
Puis encore moins.
Position du problème
Un système fermé constitué de deux particules est étudié.
L’interaction entre les deux corps est soit gravitationnelle soit électrique et de type centrale.
Elle concernera donc soit deux masses
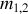 soit deux charges
soit deux charges
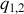 .
.
Les particules interagissent entre elles au moyen d'une énergie potentielle
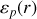 qui ne dépend que de leur distance relative : c'est le problème de Kepler.
qui ne dépend que de leur distance relative : c'est le problème de Kepler.
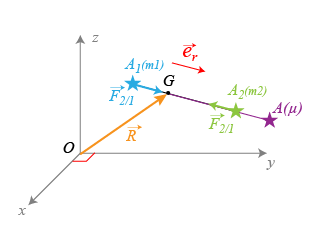
Dans un référentiel galiléen de centre
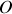 , le lagrangien est :
, le lagrangien est :
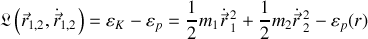
où
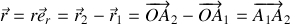
Pour
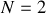 particules, la description nécessite
particules, la description nécessite
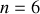 degrés de liberté.
degrés de liberté.
L'analyse directe produit 6 équations différentielles ordinaires (E.D.O) du second ordre et 12 conditions initiales (C.I.) sont nécessaires.
Lois de conservation utiles
L’intérêt de ce problème réside, entre autres, dans son aspect pédagogique puisque
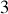 lois de conservation sont vérifiées ce qui réduit fortement la complexité du problème.
lois de conservation sont vérifiées ce qui réduit fortement la complexité du problème.
Dans l'ordre :
Les changements de variables préconisés dans le chapitre "Problèmes à 2 corps" sont également suggérés par la dépendance spatiale de l'énergie potentielle.
Ils permettaient le passage dans le référentiel du CDM selon :
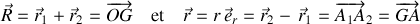
Ces nouvelles variables transforment le lagrangien ci-dessus en la somme de deux lagrangiens distincts selon :
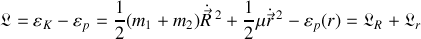
Une première simplification apparaît puisque la solution du système total est une superposition des solutions des deux sous-systèmes indépendants, pouvant être analysés séparément.
Le lagrangien
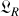 décrit le mouvement d'une particule libre de masse
décrit le mouvement d'une particule libre de masse
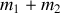 .
.
La coordonnée
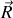 est cyclique de sorte que son impulsion associée
est cyclique de sorte que son impulsion associée
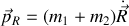 est conservée.
est conservée.
Cette grandeur est la quantité de mouvement totale correspondant à celle du centre de masse...
Cette loi de conservation permet de définir un référentiel galiléen dans lequel peut se mouvoir une particule fictive (ou relative) de masse
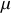 , notée
, notée
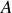 et repérée par son rayon-vecteur
et repérée par son rayon-vecteur
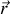 .
.
Et le mouvement de cette dernière est décrit par le second lagrangien
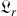 .
.
Cette analyse constitue la réduction canonique du problème à deux corps en un problème à un corps.
L'image vectorielle véhiculée par cette réduction du problème à deux corps est complétement développé dans le grain précédent.
L'analyse du lagrangien 'relatif' et de ses
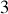 degrés de liberté est ici menée en toute généralité et en coordonnées sphériques. (voir exemple 6, chap. 1 : interaction de type Kepler)
degrés de liberté est ici menée en toute généralité et en coordonnées sphériques. (voir exemple 6, chap. 1 : interaction de type Kepler)Le lagrangien s'écrit :
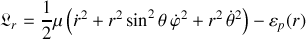
La variable angulaire
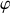 est cyclique.
est cyclique.
Ceci entraîne une invariance de l'impulsion généralisée ou moment cinétique associée à la rotation
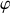 :
:
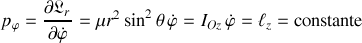
La rotation
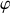 s'effectue autour de l'axe
s'effectue autour de l'axe
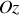 .
.
La grandeur
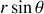 représente la distance de la particule fictive à l'axe de rotation.
représente la distance de la particule fictive à l'axe de rotation.
La grandeur précédant
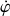 notée
notée
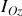 peut être assimilée à un moment d'inertie 'instantané' par rapport à l'axe de rotation
peut être assimilée à un moment d'inertie 'instantané' par rapport à l'axe de rotation
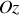 .
.
Le vecteur vitesse angulaire de cette rotation est
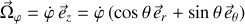 .
.
Le moment cinétique correspondant est porté par l'axe de rotation
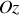 , fixe.
, fixe.
La seconde variable angulaire
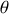 vérifie l'équation :
vérifie l'équation :
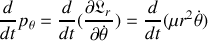
L'équation d'Euler Lagrange s'écrit :
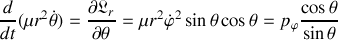
La dernière égalité n'est valide que si l'angle
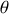 est différent de zéro, modulo
est différent de zéro, modulo
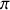 : excluant un mouvement de la particule fictive sur l'axe de rotation de
: excluant un mouvement de la particule fictive sur l'axe de rotation de
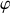 !
!
La rotation
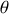 s'effectue autour de l'axe
s'effectue autour de l'axe
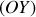 qui passe par l'origine des axes
qui passe par l'origine des axes
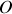 et est parallèle au vecteur unitaire
et est parallèle au vecteur unitaire
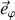 .
.
Son vecteur vitesse angulaire est donc
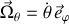 .
.
Le moment d'inertie de la particule fictive
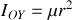 .
.
Cette équation dérive d'une grandeur scalaire issue du moment cinétique dirigé selon la direction
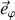 , une direction mobile.
, une direction mobile.
Le moment cinétique selon
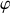 est constant mais pour la rotation
est constant mais pour la rotation
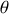 , sa conservation n'est acquise que si
, sa conservation n'est acquise que si
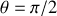 .
.
Ceci implique un mouvement de la particule fictive dans le plan horizontal
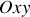 .
.
Par ailleurs le moment cinétique total est conservé au cours du mouvement puisque dans le problème à deux corps les forces sont réciproques et centrales et celui de la particule fictive l'est également.
Cette composition vectorielle des moments cinétiques correspondant aux deux rotations est donné par :
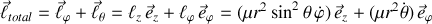
Comme vu précédemment, la dérivée du moment cinétique total par rapport au temps est nulle si les dérivées des deux contributions sont nulles.
La dérivée du terme en
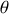 produit deux termes dont l'un vient du mouvement du vecteur unitaire
produit deux termes dont l'un vient du mouvement du vecteur unitaire
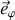 : ils devraient soit se compenser soit être simultanément nuls.
: ils devraient soit se compenser soit être simultanément nuls.
Cette dernière hypothèse est réalisée si
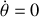 décrivant un mouvement plan (le plan de l'écliptique), perpendiculaire à l'axe
décrivant un mouvement plan (le plan de l'écliptique), perpendiculaire à l'axe
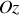 ou incliné d'un angle fixe
ou incliné d'un angle fixe
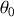 par rapport à cet axe.
par rapport à cet axe.
Toujours à titre de rappel : cette inclinaison, qui apparaît comme un degré de liberté superflu pour une particule, redevient disponible et utile quand il s'agit d'un solide.
Même si le centre de masse est dans le plan de l'écliptique (pour une planète, par exemple, mais pas pour une toupie symétrique) une inclinaison (par rapport au plan de l'écliptique) de l'axe de rotation du solide permet notamment la précession de cet axe propre : une précession générée par la rotation autour de l'axe propre.
Ainsi les points du solide qui sont hors axe propre de rotation voient leur inclinaison par rapport au plan de l'écliptique (
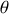 ) varier et donc redevenir un degré de liberté.
) varier et donc redevenir un degré de liberté.
Ces mouvements seront décrits plus précisément dans le troisième cours sur le solide.
Finalement la dernière équation décrit le mouvement selon :
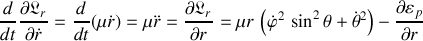
Sont reconnaissables les forces issues de 1) l'interaction à longue portée issue de l'énergie potentielle et dans le cas général 2) des entraînements produites par les rotations.
Le mouvement plan et la conservation du moment cinétique de la rotation
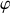 peuvent alors être intégrées.
peuvent alors être intégrées.
Les résolutions directe et graphique du chapitre "Problème à deux corps" du grain précédents sont reproduites par le formalisme lagrangien.
En résumé, pour la réduction canonique du problème de Kepler de deux corps à un seul, ont été utilisées :
l'invariance par translation d’espace (variables d’espace cycliques) : l’impulsion totale des deux corps est conservée.
l'invariance par rotation (variables angulaires cycliques): le moment cinétique total est constant.
Le système est fermé :
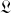 ne dépend pas explicitement du temps, entraînant la conservation de l’hamiltonien ou énergie mécanique totale.
ne dépend pas explicitement du temps, entraînant la conservation de l’hamiltonien ou énergie mécanique totale. Cette partie apparaît lors de la résolution graphique du problème de la particule fictive. (voir grain précédent, chapitre "problèmes à deux corps").




