Pour des raisons pédagogiques de simplicité, une seule contrainte
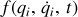est considérée voire isolée. Toutes les autres ont permis d'exprimer
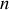degrés de liberté notés :
.
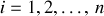La contrainte ne permettant pas d'aller au delà dans la réduction de la dimension du problème
peut être non holonome ou même holonome, et complexe par exemple.
La méthode qui suit reste la même.
Méthode : Construction du lagrangien sous contrainte
Le lagrangien du système qui utilise les
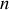degrés de liberté, et les contraintes associées, est noté :
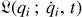
La contrainte additive
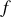est introduite dans le formalisme par construction d'un nouveau lagrangien : le lagrangien sous contrainte
Fondamental : Lagrangien sous contrainte
Le lagrangien du système sous la nouvelle contrainte
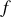est construit selon le schéma :
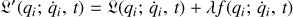
où
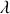est le multiplicateur de Lagrange.
Il introduit multiplicativement l'équation de la contrainte.
Explication : Remarques et analyse.
Le lagrangien sous contrainte présente une "correction additive" au lagrangien initial.
Le lagrangien initial est constitué de grandeurs, énergies cinétique et potentielle, elles-mêmes additives.
→ La dimension du produit
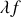doit être une énergie.
Ainsi,
Tout comme pour le formalisme de Lagrange du premier type, ce multiplicateur apparaît comme une mise à l'échelle de l'effet de la contrainte, le lagrangien ayant une dimension énergétique.
De plus, ce nouveau paramètre
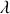est inconnu et devra être déterminé.
Fondamental : Inconnues du problème sous contrainte.
Le bilan du nombre d'inconnues est
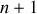: les
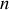variables indépendantes (coordonnées généralisées) du problème et le multiplicateur.
Or les équations d'Euler Lagrange ne peuvent fournir que
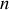équations différentielles.
L'équation de la contrainte
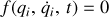devrait être la
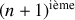équation.
Méthode : Équations modifiées d'Euler Lagrange
Les
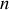degrés de liberté permettent de déduire les équations d'Euler Lagrange pour le lagrangien contraint :
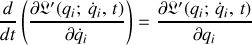
dérivées de l'optimisation de l'action, selon la méthode explicitée au chapitre II, paragraphe C.
Les
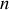équations obtenues sont paramétrées par l'inconnue
.
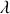En effet, les solutions obtenues sont telles que :
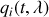et
.
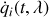Ces solutions, reportées dans l'équation de la contrainte, permettent de déduire une équation pour le paramètre
.
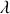Une fois résolue, la valeur convenable du paramètre
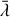est obtenue :
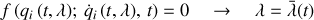
Ainsi les trajectoires contraintes s'écriront :
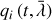
Propriété : Autre formulation des équations modifiées d'Euler Lagrange.
La contrainte non holonome s'exprimant toujours selon :
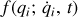, dans le cas le plus général, les équations d'Euler Lagrange sont développées :
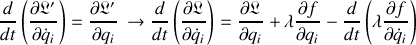
Ceci correspond à
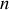équations différentielles du second ordre.
Il faudra donc ajouter l'équation de la contrainte
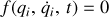pour compléter le système d'équations à résoudre et permettre ainsi d'accéder à toutes les inconnues, le paramètre
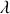compris.
La forme additive de la construction du lagrangien sous contrainte permet une généralisation directe à un nombre
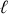de contraintes.
L'ajout d'autant de termes en
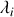et
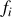que nécessaires s'effectue de façon similaire.
Cette richesse du formalisme lagrangien, et sa simplicité, apparaît dès la construction du lagrangien avec ses grandeurs énergétiques additives et se répercute sur les équations d'Euler Lagrange obtenues.
Les contraintes qui s'ajoutent "perpétuent" ces propriétés.
De plus la possibilité de construire des classes de contraintes pour des classes de solutions émerge.
L'analyse du lagrangien dans un référentiel non galiléen, dans le chapitre qui suit, présente une similarité avec cette approche du lagrangien sous contrainte.
Mais dans ce cas, nul besoin de multiplicateurs de Lagrange puisque les contraintes de l'entraînement ont déjà les dimensions adéquates.
Complément : 1. Contraintes holonomes et multiplicateurs de Lagrange.
Lorsque la contrainte est holonome sans pouvoir (ou vouloir) réduire le nombre de degrés de liberté, une forme simplifiée des équations d'Euler- Lagrange est accessible.
Elle correspond à un formalisme du premier type appliqué aux coordonnées généralisées et non plus au second principe de Newton.
La méthode est ici présentée en deux étapes.
1) De façon générale, si une contrainte existe, les déplacements virtuels infinitésimaux sur les
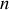degrés de liberté ne sont pas indépendants.
Et pour une contrainte donnée, une relation les reliera qui pourra s'écrire :
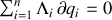
Les coefficients du développement y sont notés
.
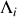Lorsque la contrainte est holonome, cette relation est intégrable et s'écrit :
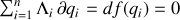
2) L'application du principe de moindre action à un lagrangien modifié par l'introduction des multiplicateurs de Lagrange associées aux contraintes notées comme ci dessus et
- dans une notation en accélérations et forces généralisées, les équations d'Euler Lagrange vont s'écrire :
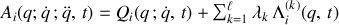
pour chaque coordonnée généralisée
.
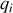Il est utile de noter que :
la généralisation à
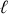contraintes a été intégrée.
la particularité de la contrainte holonome
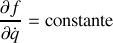permet de simplifier la forme générale développée précédemment.Surtout si le paramètre
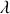est indépendant du temps.la similarité avec le formalisme du premier type est flagrante si l'expression
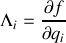est interprété comme une composante du gradient.
Complément : 2. Régime stationnaire et optimisation.
Pour les situations où le temps est figé ("le temps mécanique est absent"), ce dernier n'intervient pas dans la description, ni dans les équations ci-dessus.
Ceci correspond à une analyse d'états stationnaires puisque les impulsions généralisées sont conservées.
Une autre façon d'exploiter, et de voir, les équations d'Euler Lagrange est de les écrire sous la forme :
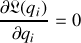
Ne subsistent que les variables généralisées décrivant le système, avec ou sans multiplicateurs de Lagrange.
Plus généralement, pour un système physique décrit par une fonctionnelle
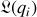liant des grandeurs mesurables
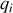entre elles, la vérification de ces égalités caractérise l'existence d'un extremum dans l'espace (lagrangien, coordonnées) : l'axe des vitesses généralisées est tel que
.
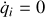C'est le cas des potentiels thermodynamiques mais également de l'utilité ou la satisfaction d'un consommateur, du profit d'un producteur...
Lorsque le lagrangien d'un système mécanique est caractérisé par des dépendances séparées entre vitesses et coordonnées généralisées, d'une part, et respectivement énergie cinétique et énergie potentielle d'autre part, le lagrangien peut être remplacé par l'énergie potentielle.
Cette situation correspond, par exemple, à la description des états d'équilibre pour un système mécanique où l'énergie potentielle, seule, dépend des coordonnées généralisées : états caractérisés par un optimum de cette énergie.
De même les potentiels thermodynamiques décrivent ces états en fonction des variables qui leurs sont caractéristiques.
La stabilité ou instabilité (locale) des états est alors portée par la dérivée seconde (pour une variable ou un ensemble de variable).
Elle exprime le signe de la courbure :
positive, l'état est stable,
négative, il est instable
nulle, l'état est métastable ou indifférent. La dérivée d'ordre suivant peut permettre de trancher.
Complément : 3. De l'optimisation sous contraintes
Lorsque les variables décrivant un système sont définies et notées :
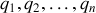, ainsi que la fonctionnelle qui les associe
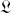, l'apparition de contraintes
est également traité avec des multiplicateurs de Lagrange.
Une nouvelle fonctionnelle est élaborée selon :
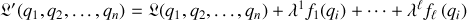
de sorte que les conditions d'optimisation sous contrainte, ou équations d'Euler Lagrange 'stationnaires' s'écrivent :
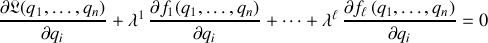
Des équations auxquelles il faut ajouter celles des contraintes.
L'optimisation sous contraintes apparaît comme un cas particulier du formalisme lagrangien général développé pour la mécanique.
Elle est utilisée dans d'autres domaines scientifiques dont l'économie.
Exemple : Physique statistique et multiplicateurs de Lagrange.
L'utilisation des multiplicateurs de Lagrange permet d'optimiser sous contraintes une fonction de distribution et de déduire la constante de Boltzmann.
Ainsi
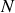particules ou molécules (
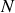fixe) sont susceptibles d'occuper les états d'énergie suivants :
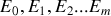
Ces particules se repartissent sur les différents niveaux selon une distribution de particules
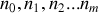
Le nombre de façons de distribuer les
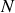particules sur les
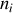différents états d'énergie est alors :
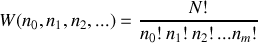
Les propriétés du logarithme et la formule de Stirling (
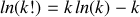) permet le passage à la forme suivante de
:
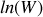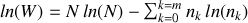
Il existe une distribution
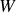particulière tel que le système est pratiquement toujours dans cette configuration de sorte que les propriétés macroscopiques sont celles de cette configuration dominante.
Cette distribution optimisée est celle qui distribue les paquets de particules (les
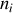) sous les deux conditions suivantes :
le système est fermé et conserve le nombre de particules : (
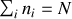) et les configurations autorisées sont celles correspondant à une valeur définie de l'énergie totale du système soit
.
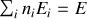Si
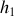, la contrainte sur le nombre de particules est associée à un multiplicateur de Lagrange noté
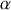et si
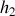, la contrainte sur l'énergie est associée au multiplicateur
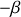, la méthode de l'optimisation sous contraintes, appliquée à
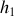permet d'obtenir la relation, dite distribution de Boltzmann :
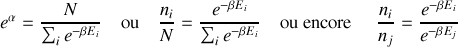
Cette dernière est la formule du rapport de Boltzmann qui permet de prédire les populations des états d'énergies .
La grandeur
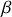est obtenue en appliquant la contrainte liée à l'énergie et en la comparant à l'énergie interne d'un gaz monoatomique qui vaut
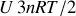(à sa valeur pour
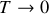près) :
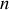est le nombre de moles.
Par la distribution de Boltzmann, la valeur d'énergie interne obtenue est :
.
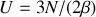Par comparaison le multiplicateur de Lagrange
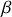vaut
.
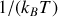