Énoncé
Cet exercice est à traiter avec un multiplicateur de Lagrange pour exploiter l'équation de la contrainte.
Une sphère de masse totale
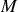, de rayon
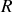, roule sans glisser sur un plan incliné d'un angle
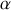par rapport à l'horizontale (et ici, fixe).
Donner l'accélération du CDM de la sphère ainsi que le multiplicateur de Lagrange associé à la condition de roulement sans glissement.
Quelle est sa signification ? (2 réponses sont possibles du fait de la contrainte holonome)
Comme il s'agit d'un solide, une comparaison nécessaire avec le point matériel qui, lui, ne roule pas et dont la solution pour l'accélération est connue.
Sinon un cas à traiter au préalable pour la mise en route.
Pour un solide : l'énergie cinétique est le fruit d'une translation du CDM et d'une rotation de la sphère autour d'un de ses axes.
L'énergie potentielle de pesanteur est rapportée au CDM. (→ Comme pour un point matériel)
Écrire l'équation de la contrainte pour déduire le lagrangien contraint. (→ Cours ci-dessus)
Donner le système d'équations à résoudre.
La figure (Fig. 5) peut être reconsidérée avec les modifications suivantes :
Le plan est fixe donc
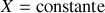
Le point matériel représenté par un bloc est remplacé par une sphère de rayon
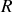. Les notations sont à réadapter.
Deux degrés de liberté : la rotation
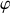et
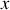, le déplacement du CDM le long de l'axe incliné.
Quelle relation les associe ? → normalement cela libère un degré de liberté.
Cette contrainte est holonome.
La contrainte choisie peut être
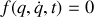ou
.
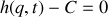En essayant les deux, le rôle du paramètre
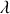peut être explicité.
La rotation a lieu par rapport à un axe passant par le CDM : moment d'inertie de la sphère par rapport à cet axe noté,
.
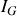Sa détermination fait, soit partie d'une question préliminaire soit peut s'évaluer à la fin... si application numérique ou pour l'excellence d'une réponse analytique "tout compris".
La sphère démarre d'une hauteur H sur le plan incliné. Utile pour écrire l'énergie potentielle.
Entre point matériel et solide.
Pour comparer avec le point matériel dont le mouvement est produit par la composante du poids
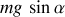, son accélération est
.
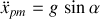Elle est issue du second principe de Newton :
.
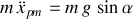L'effet d'inertie est produit par la seule masse du point matériel : elle n'apparaît plus dans l'accélération.
La sphère cumule les mouvements de translation et rotation : elle subit donc deux effets inertiels, l'un porté par sa masse, l'autre par son moment d'inertie.
L'origine du mouvement est toujours la pesanteur.
La composante de la force qui le produit est :
.
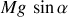→ L'accélération du CDM est :
.
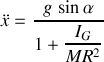Le paramètre
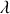, et la contrainte qu'il véhicule, sont donc associés à l'effet de la rotation.
A l'origine de la rotation, la force de contact (et de frottement) qui accroche la sphère au niveau du plan... et qui explique une accélération de translation de la sphère... inférieure à celle du point matériel.
En comparant avec le point matériel, le second principe de Newton selon la direction de la pente
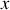devrait intégrer la composante de la force de contact
.
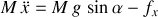L'équation d'Euler Lagrange pour la variable
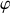devrait redonner le théorème du moment cinétique avec un moment de force qui ne peut être que celui de la force de contact, le moment du poids étant nul.
Surtout si l'équation de la contrainte est exprimée sous la forme :
→
.
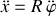Pour déduire
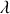et sa signification, il faut écrire le lagrangien contraint
Solution avec la contrainte h
Le lagrangien contraint de la sphère qui roule :
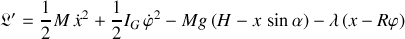
Apparaissent successivement :
L'énergie cinétique de translation
L'énergie cinétique de rotation
L'énergie potentielle de pesanteur
La contrainte et son multiplicateur dans sa version
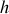. Le signe "moins" est de confort.
Une conditions initiale
n'apporte rien au lagrangien.
L'équation d'Euler Lagrange pour la variable
:
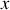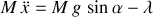
donne directement la signification du multiplicateur de Lagrange : le paramètre est le module de la force de liaison.
Le signe "moins" justifie le module.
Celle pour la variable
:
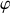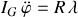
n'est autre que le théorème du moment cinétique, en norme : la variation temporelle de ce dernier est produite par le moment de la force de liaison.
A ces deux équations, s'ajoute la contrainte sous la forme :
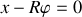ou encore mieux :
.
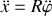L'accélération de la translation est déduite, identique à celle précédemment établie.
Le paramètre de la contrainte est tel que :
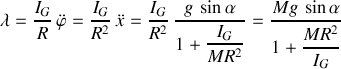
Il s'agit d'une force, opposée à la composante du poids à l'origine du roulement , mais qui lui est inférieure en intensité.
→ Un bilan des forces favorable au déplacement.
Pour une sphère, le moment d'inertie vaut :
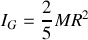de sorte que l'accélération du CDM vaut
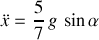et le multiplicateur de Lagrange
.
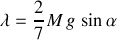Complément : Solution avec la contrainte f
L'accélération linéaire de la sphère ne doit pas être modifiée.
Seule la signification de la contrainte risque de changer.
L'équation de la contrainte dans sa version
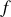s'écrirait :
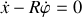
Le lagrangien contraint s'écrit alors :
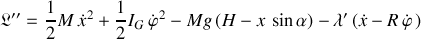
Par souci de cohérence, le signe "moins" a été conservé.
Les équations d'Euler Lagrange sont modifiées selon :
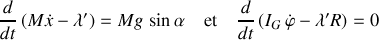
La dimension du paramètre est cette fois-ci une impulsion (quantité de mouvement), et son effet produit une "chute" d'impulsion.
Contrairement au cas
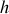, la nécessité d'une dépendance temporelle du multiplicateur de Lagrange est explicite puisqu'il est susceptible de donner une force.
Pour autant, la valeur de l'accélération de translation est identique à celle dérivée.
Mais la forme du paramètre est modifiée.
Le lagrangien est une énergie. La contrainte étant proportionnelle à une vitesse, le multiplicateur de Lagrange devient une impulsion.
L'équation pour
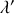s'écrit :
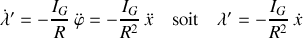
où
le confort du signe du paramètre a été abandonné,
l'accélération de translation, constante, doit être intégrée pour accéder au paramètre,
et, pour la sphère,
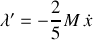, soit
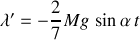si aucune vitesse initiale n'est présente.
Finalement,
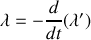
Conclusion
La simplicité de cet exemple permet de saisir toutes les nuances du formalisme, d'en moduler les difficultés et d'utiliser le formalisme vectoriel... comme une aide.
Le mouvement étant plan, une autre contrainte a été appliquée
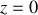réduisant le nombre de degrés de liberté de
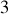à
.
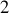Dans l'analyse des formes de contrainte, le temps joue encore son rôle particulier de paramètre continu.
Complément : Et avec un plan incliné non fixe ?
Une fois assimilée la notion de contrainte, dans sa globalité, l'étape suivante est de libérer le plan incliné pour pouvoir analyser l'influence éventuelle du degré de liberté supplémentaire, dû au mouvement du plan
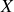, sur le multiplicateur de Lagrange.
Exemple : Suggestion d'exemple complémentaire
Reprise de l'exercice "chafouin" du chapitre 1 B.2, concernant la bille dans le rail qui tourne avec une vitesse angulaire
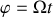, par exemple.
Cet exercice peut être traité avec
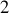degrés de liberté et la contrainte sur la vitesse angulaire.
Le multiplicateur de Lagrange associé à la contrainte apparaît immédiatement comme le moment de force à l'origine de la rotation et ce quelle que soit la vitesse imposée par le moteur.
