Certaines contraintes, y compris holonomes, sont quelquefois trop complexes pour permettre l'émergence des nouvelles coordonnées généralisées, en nombre réduit.
D'autres contraintes non holonomes, comme les inégalités, n'offrent pas de moyen de réduire le nombre de degrés de liberté.
Dans ces cas, les coordonnées initiales, en trop grand nombre, sont conservées et la question qui se pose concerne l'impact des contraintes sur le mouvement du système et leur intégration dans le modèle.
La réponse à cette question figure dans le développement d'une méthode générale d'extension du formalisme lagrangien.
Elle consiste à élaborer un lagrangien sous contraintes et à lui appliquer le principe de moindre action pour en déduire des équations d'Euler Lagrange modifiées.
L'introduction d'une inconnue supplémentaire par contrainte, nommé multiplicateur de Lagrange, permet d'adapter la contrainte au formalisme, de donner un sens physique à l'équation de la contrainte.
La notation
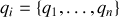est sous entendue ci après.
A titre de rappel :
Une contrainte
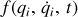est holonome si elle vérifie la propriété suivante :
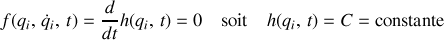
Cette définition
exprime notamment une dépendance linéaire en vitesse,
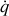, de la contrainte
,
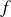est similaire à la propriété des lagrangiens, associée à la relation de jauge développée dans un exemple précédent. Même nulle, elle existe.
La contrainte non holonome est caractérisée par les propriétés suivantes :
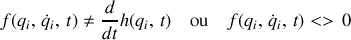
Plus généralement, un système est décrit par un ensemble de contraintes notées
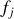dont certaines sont holonomes.
Le mouvement du système soumis aux contraintes holonomes est décrit par un lagrangien
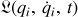à
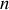degrés de liberté et
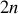variables.
Il restera à ajouter l'effet des contraintes qui restent, non holonomes ou holonomes complexes (inexploitables).
Le traitement direct des contraintes non holonomes pour réduire la dimension du problème étant impossible (ou non souhaitée), il faut construire le lagrangien qui tienne compte de ces contraintes à partir du lagrangien précédent.
Une remarque :
Dans l'exemple qui suit le développement de la méthode, la contrainte utilisée est holonome et aisément intégrable.
Mais pour des raisons pédagogiques, cette propriété ne sera pas exploitée pour deux raisons :
la signification du multiplicateur de Lagrange peut être explicitée, selon le choix effectué,
et pour cela, la pratique du formalisme vectoriel (devenu traumatisant pour les dernières générations d'étudiants) sous couvert de multiplicateur de Lagrange apparaîtra comme "tellement évidente".
Ainsi que les réponses sur les contraintes et les liaisons qui deviennent également "tellement évidentes"... à postériori.
