Les intervalles d'espace et de temps associés à deux évènements n'étant pas invariants lors du passage d'un référentiel inertiel à l'autre, sur quelle grandeur peuvent se mettre d'accord les deux observateurs O et O' ?
On peut raisonner en faisant appel à une analogie euclidienne. La figure ci-après illustre que lors d'une rotation d'espace, les coordonnées des évènements E_1 et E_2 vont varier, mais que la distance est invariante (elle ne dépend pas de l'angle de rotation) :
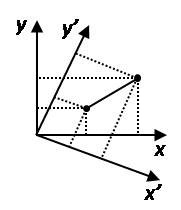
Il faut donc généraliser la notion de distance, dans un espace élargi à quatre dimensions, en combinant les intervalles de temps et d'espace.
On introduit la grandeur invariante s_{12}^2, qui est indépendante de la vitesse relative entre les deux observateurs O et O' :
\displaystyle{ \begin{array}{c c c} s_{12}^2 & = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2- (y_2 - y_1)^2 - (z_2 - z_1)^2 \\ & = c^2 (t'_2 - t'_1)^2 - (x'_2 - x'_1)^2 - (y'_2 - y'_1)^2 - (z'_2 - z'_1)^2 \end{array}
On démontre facilement la seconde égalité à l'aide des transformations de Lorentz-Poincaré : la grandeur s_{12}^2 est invariante par changement de référentiel inertiel.
L'intervalle s_{12}^2 peut-être positif, nul ou négatif :
s_{12}^2 > 0 : intervalle de genre temps
s_{12}^2 = 0 : intervalle de genre lumière
s_{12}^2 < 0 : intervalle de genre espace
Le signe de s_{12}^2 est aussi invariant. La signification physique de cette classification est discutée au paragraphe au dessus.
On peut aussi écrire l'intervalle s_{12} entre les évènements E_1 et E_2 comme :
s_{12} = \sqrt{(\Delta x^0)^2 - \sum_{i = 1}^3 (\Deltax^i)^2}
avec x^0 = ct, x^1 = x, x^2 = y, x^3 = z.
Il est d'usage en mathématique de distinguer deux types de composantes d'un vecteur : covariantes et contravariantes. Sans entrer ici dans le détail du formalisme, signalons que l'on note les composantes contravariantes d'un vecteur x^{\mu}, et les composantes covariantes de ce même vecteur x_{\mu} (\mu = 0 - 3). Nous travaillons en relativité restreinte avec les composantes contravariantes des vecteurs.
L'intervalle élémentaire ds^2 est défini par :
ds^2 = (dx^0)^2 - \sum_{i = 1}^3 (dx^i)^2
La forme quadratique donnée par la relation ds^2 = (dx^0)^2 - \sum_{i = 1}^3 (dx^i)^2 permet de définir une structure métrique dans un espace de Riemann à 4 dimensions :
ds^2 = \sum_{\mu = 0}^3 \sum_{v = 0}^3 dx^{\mu}g_{\muv}dx^v
g_{\muv} est un tenseur (une matrice) diagonal dont les éléments prennent ici les valeurs :
\displaystyle{ g_{\muu} = \left(\begin{array}{c c c c} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\0 & 0 & 0 & -1\end{array}\right)}
Un espace à quatre dimensions muni de la métrique \displaystyle{ g_{\muu} = \left(\begin{array}{c c c c} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\0 & 0 & 0 & -1\end{array}\right)} est appelé espace de Minkowski.