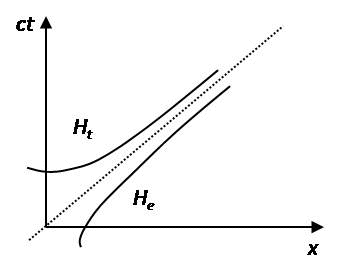
Lors du passage d'un référentiel inertiel \mathcal{R}~ à un référentiel inertiel \mathcal{R}', on peut écrire c^2t^2 - x^2 = c^2 t'^2 - x'^2. Tous les évènements E caractérisés par la même valeur de l'invariant s^2, sont situés sur une même hyperbole, H_t~ si l'intervalle est du genre temps, et H_e~ s'il est du genre espace.

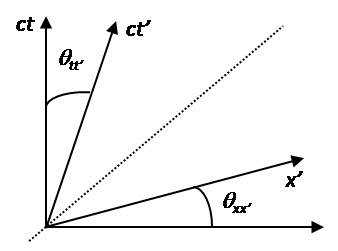
Le diagramme espace-temps introduit par Minkowski en 1908 consiste à représenter, dans un même plan, les coordonnées (ct,x) et (ct',x') d'un évènement E :

\overrightarrow{oE} = ct \vec e_t + x\vec e_x = ct' \vec e_{t'} + x' \vec e_{x'}

Cela revient à poser la question de comment les transformations spéciales de Lorentz transforment-elles un repère (ct,x) en un repère (ct',x') ? On choisit pour \mathcal{R} un repère cartésien orthonormé :

∥\vec e_x\parallel= ∥\vec e_t\parallel= 1; \vec e_x . \vec e_t = 0

L'équation du vecteur \vec e_{t'} associé à l'axe ct' est obtenu en posant x'= 0 dans \overrightarrow{oE} = ct \vec e_t + x\vec e_x = ct' \vec e_{t'} + x' \vec e_{x'} et \displaystyle{ \left\{ \begin{array}{c c c c} ct = \gamma_e (ct' + \beta_ex') \\ x = \gamma_e(\beta_e ct' + x') \\ y = y' \\ z = z' \end{array} :

\vec e_{t'} =  \gamma_e \vec e_t + \gamma_e \beta_e \vec e_x

De façon similaire on obtient :

\vec e_{x'} = \gamma_e \beta_e \vec e_t + \gamma_e \vec e_x

On peut voir qu'une transformation spéciale de Lorentz transforme un repère cartésien en un repère non cartésien :

\parallel\vec e_{x'}\parallel= \parallel\vec e_{t'}\parallel= \gamma_e (1 + \beta_e^2)^{\frac12} = (\frac{1 + \beta_e^2}{1 - \beta_e^2})^{\frac12} \ge 1

\displaystyle{ \begin{array}{c c c} \cos \theta_{x't'} = \frac{\vec e_{x'}. \vec e_{t'}}{\parallel\vec e_{x'}\parallel~\parallel\vec e_{t'}\parallel} = \frac{2\beta_e}{1 + \beta_e^2} & \cos \theta_{xx'} = \frac{\vec e_{x}. \vec e_{x'}}{\parallel\vec e_{x}\parallel~\parallel\vec e_{x'}\parallel} = (1 + \beta_e^2)^{-\frac12} = \cos \theta_{tt'} \\ & \\ & \end{array}