On se pose la question de savoir comment, dans un espace à deux dimensions (on ignore les coordonnées y et z), représenter l'invariant s_{12} ? Pour cela considérons des évènements repérés dans le référentiel d'inertie \mathcal{R} d'origine o et de coordonnées (ct,x). Un mobile physique partant de o voit la valeur de sa vitesse limitée par c, sa position sera donc caractérisée par la relation |x| < c |t|. L'espace – temps est donc séparé en deux régions par les droites bissectrices x = \pm ~ct. La grandeur et le signe de l'intervalle s_{12}^2 = c^2t^2 - x^2 étant conservés, les deux droites bissectrices sont associées aux trajectoires des rayons lumineux issus de o, elles définissent le cône de lumière. L'intérieur du cône est du genre temps (s_{12}^2 > 0), l'extérieur est du genre espace (s_{12}^2 < 0).

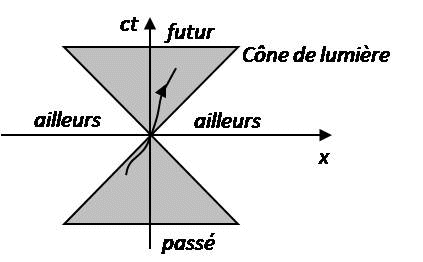
Notons quelques propriétés remarquables :

• Tout point à l'intérieur du cône de lumière pourra être atteint dans le futur par un mobile physique parti de l'origine (le mobile se déplace à une vitesse permise, inférieure à c).

• Tout point situé sur le cône de lumière pourra être atteint par un flash lumineux (qui se propage à la vitesse c).

• Un point situé en dehors du cône de lumière ne pourra jamais être atteint à partir de l'origine (il devrait se déplacer à une vitesse supérieure à c).

On peut alors établir un lien remarquable entre géométrie et causalité :

• Les évènements situés à l'intérieur du cône de lumière supérieur peuvent avoir été causés par un évènement antérieur, situé par exemple en o.

• L'évènement situé en o peut avoir été causé par tout point situé dans le cône de lumière inférieur.

• Il ne peut y avoir aucune relation causale entre l'origine et un point situé à l'extérieur du cône de lumière.

Comme l'intervalle s_{12}^2 est conservé lors du passage d'un référentiel inertiel \mathcal{R} à un référentiel inertiel \mathcal{R}' (on peut écrire c^2t^2 - x^2 = c^2t'^2 - x'^2), on peut dire que la séquence temporelle de deux évènements séparés par un intervalle du genre temps est une donnée objective. En clair cela signifie que si un observateur dit « E_2 se passe après o », tous les observateurs seront d'accord, même s'ils ne mesurent pas le même intervalle de temps entre les deux évènements.

En effet, soit E_1 en o. Pour E_2 soit ct > 0 et ct^2 - x^2 > 0. Par \displaystyle{ \left\{ \begin{array}{c c c c} ct' = \gamma_e (ct - \beta_ex) \\ x' = \gamma_e(-\beta_e ct + x) \\ y' = y \\ z' = z \end{array}, ct' = \gamma_e(ct - \beta_e x).

Si x < 0, ct'>0. Si x > 0, on a toujours |x| < |ct| (intervalle de genre temps) et \beta_e < 1, donc on a toujours ct' > 0.

Dans un intervalle de genre espace, ct' < 0 est possible car |x| > |ct| : la séquence temporelle n'a plus de sens objectif.