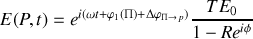Présentation du système
Nous considérons de nouveau le cas d'une lame à faces parallèles d'épaisseur
que nous utilisons en transmission. Un rayon incident arrive sur la lame et subit à l'intérieur de celle-ci des réflexions multiples ainsi qu'une série de transmissions. A la sortie tous les rayons transmis sont parallèles entre eux et présentent un déphasage qui va croissant avec le nombre de réflexion par rapport au rayon
transmis sans réflexion en
. Ces rayons qui convergent à l'infini peuvent être focalisés en un point
d'un écran en utilisant une lentille mince convergente de distance focale
comme on peut le voir sur la figure 40.
Remarque :
Le système présente une symétrie de révolution autour de l'axe optique de la lentille mince passant par la source et la figure d'interférence présente donc la même symétrie. Elle est constituée d'anneaux concentriques centrés sur
.
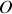Calcul de la différence de marche
Le rayon
et le rayon
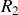sont parallèles entre eux. Pour connaître leur différence de marche il convient d'établir la différence de chemin optique parcourue par les deux ondes à l'issue de leur division en
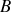où ils sont en phase (voir figure 40).
Remarque :
A partir des points
et
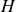les deux rayons parcourent les mêmes chemins optiques. La différence de marche entre les rayons
et
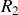issus de
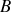lorsqu'ils atteignent les points
et
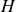est donc
soit
En utilisant la loi de Snell-Descartes,
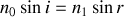, nous obtenons
La différence de marche entre le rayon 2 et le rayon 1 aux points
et
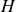correspond à une différence de phase qui est égale à
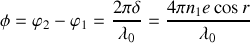
Complément :
Il n'y a pas de changement de phase à la réflexion car les réflexions sont de même nature.
Le problème est identique pour les rayons
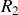et
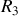qui sortent de la lame aux points
et
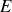. La différence de phase entre ces deux rayons est donc
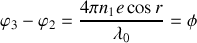
Il s'ensuit que la différence de phase entre le rayon
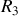et le rayon
est
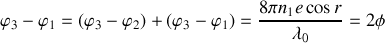
Par itération nous voyons que le rayon
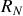sera déphasé par rapport au rayon
de
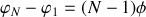
Une bonne façon de voir comment les ondes se déphasent les unes par rapport aux autres est de prendre la référence de phase sur le plan
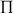perpendiculaire au rayon
passant par le point du dioptre ou sort ce rayon. Au delà du plan
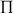nous admettrons que tous les rayons parcourent rigoureusement le même chemin optique pour aller en
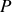(ceci est une conséquence des propriétés des lentilles minces). Pour aller de
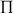en
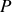les rayons subiront tous le même déphase
.
Attention :
Sur le plan
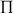, les rayons ont une phase qui dépend du rayon considéré et qui vaut
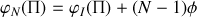. En
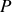les rayons seront donc déphasés de
Amplitude des rayons transmis
Soit
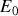l'amplitude du champ incident ; le champ transmis en
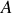dans la lame est
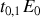où
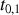est le coefficient de transmission du dioptre air-lame. En
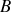une partie de l'onde transmise est réfléchie sur le dioptre lame-air et l'autre partie est transmise dans l'air. L'amplitude du champ est affectée à chaque réflexion et transmission ; ainsi le rayon
sortant en
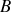a pour amplitude
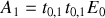
Le rayon
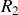subit deux réflexions supplémentaires avant de sortir en
et a une amplitude
Si l'on appelle
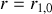le coefficient de Fresnel du dioptre 1,0, les rayons successifs auront donc pour amplitude
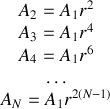
Amplitude de l'onde résultante
Le champ résultant au point
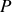d'observation sur l'écran est obtenu en sommant tous les champs provenant des différents rayons. Nous considérons ici des champs scalaires
En tenant compte des amplitudes et des phases des rayons en
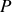nous avons
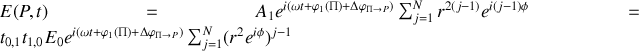
Il s'ensuit que l'amplitude du champ en
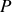est donnée par une suite géométrique de raison
. Le calcul de cette suite est classique et conduit à
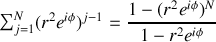
En adoptant les notations suivantes
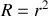et
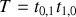, nous aboutissons à
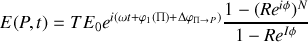
Comme le coefficient
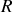est petit
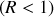le terme
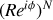devient rapidement négligeable dès que
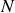excède 10 et le champ en
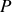devient
