Principe
Remarque :
L'interféromètre de Perot-Faby est une cavité optique résonante. Ce type de cavité a trouvé à la découverte de l'effet Laser une utilité toute naturelle pour permettre l'entretien des oscillations lumineuses engendrées dans la cavité.
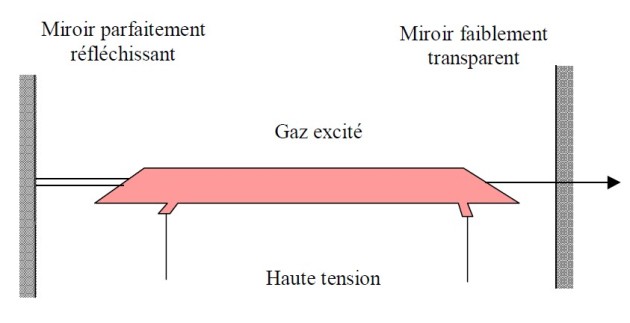
Pour simplifier un laser est constitué de deux miroirs séparés d'une distance
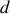 ; l'un des deux miroirs est parfaitement réfléchissant et l'autre est légèrement transparent pour laisser s'échapper le rayonnement lumineux (voir 45). A l'intérieur de la cavité formée par les deux miroirs se trouve un gaz sous faible pression. Le gaz est excité par une décharge électrique. Par exemple dans un laser He-Ne, le gaz est constitué de
; l'un des deux miroirs est parfaitement réfléchissant et l'autre est légèrement transparent pour laisser s'échapper le rayonnement lumineux (voir 45). A l'intérieur de la cavité formée par les deux miroirs se trouve un gaz sous faible pression. Le gaz est excité par une décharge électrique. Par exemple dans un laser He-Ne, le gaz est constitué de
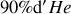 et de
et de
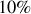 de
de
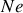 sous une pression totale de
sous une pression totale de
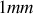 de
de
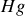 . La tension entre les deux éléctrodes est de l'ordre de
. La tension entre les deux éléctrodes est de l'ordre de
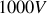 ce qui permet d'amener par collision les électrons des atomes dans des niveaux excités.
ce qui permet d'amener par collision les électrons des atomes dans des niveaux excités.
Dans le cas de ce laser, il y a deux types d'atomes. On peut supposer que les atomes
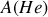 sont dans un état excité et qu'il peuvent transférer leur énergie par collision aux atomes
sont dans un état excité et qu'il peuvent transférer leur énergie par collision aux atomes
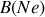 pour les amener dans un état excité. On dit alors que l'on a une collision résonante. La probabilité d'observer ce phénomène est régie par les règles de la mécanique quantique et l'on montre qu'elle est d'autant plus grande que la différence des niveaux d'énergie est faible. C'est pourquoi on utilise ce type de mélange car les niveaux
pour les amener dans un état excité. On dit alors que l'on a une collision résonante. La probabilité d'observer ce phénomène est régie par les règles de la mécanique quantique et l'on montre qu'elle est d'autant plus grande que la différence des niveaux d'énergie est faible. C'est pourquoi on utilise ce type de mélange car les niveaux
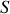 de l'
de l'
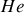 sont très proches des
sont très proches des
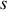 et
et
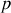 du
du
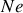 . La transition du niveau
. La transition du niveau
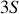 à
à
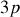 du
du
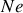 produit une raie rouge intense de longueur d'onde
produit une raie rouge intense de longueur d'onde
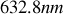 .
.
Rappel :
Einstein a montré en 1917 que si un atome est déjà dans un état excité le photon incident ne peut être absorbé mais qu'il provoque la désexcitation de l'atome avec émission d'un photon de même énergie qui a les propriétés suivantes
le train d'onde associé au photon induit est en phase avec celui du photon incident
il est émis dans le même sens et avec la même polarisation.
Ceci constitue le phénomène d'émission induite ou émission stimulée représentée sur la figure 46.
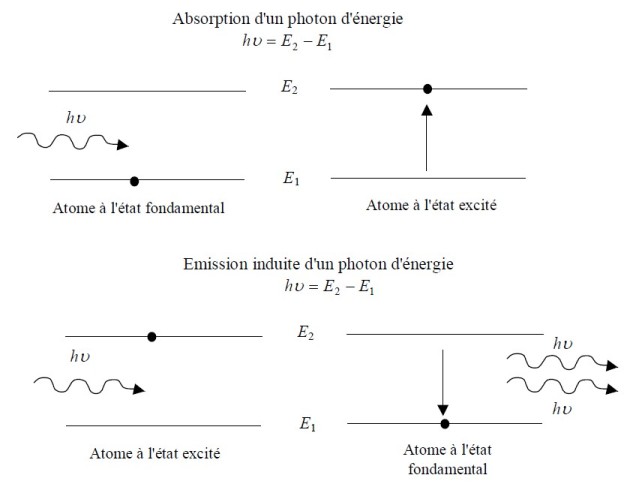
Le phénomène d'émission induite est très rare dans des sources classiques qui fonctionnent sur le principe de l'émission radiative spontanée. Dans les lasers on s'arrange pour amener une grande partie des atomes dans un état excité. Un photon spontané émis dans un tel milieu produit une véritable cascade de photons induits ayant tous la même phase et la même direction de propagation que le photon incident.
Attention :
Pour fonctionner correctement un laser doit donc être constitué de trois éléments :
un milieu actif dans lequel on réalise l'inversion de population, c.a.d. l'excitation d'une grande partie des atomes
une cavité résonnante (
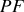 ) qui favorise l'émission induite pour peu que les ondes soient en phase à chaque réflexion.
) qui favorise l'émission induite pour peu que les ondes soient en phase à chaque réflexion.
une source d'énergie qui permet l'inversion de population et qui évite les pertes.
Durée de vie
Le rayonnement émis se propage dans la cavité et est réfléchi par les miroirs. Si l'on appelle
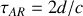 le temps mis par un rayon pour effectuer un aller-retour dans la cavité, on conçoit que l'intensité puisse augmenter par sauts de
le temps mis par un rayon pour effectuer un aller-retour dans la cavité, on conçoit que l'intensité puisse augmenter par sauts de
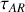 si les miroirs sont assez réfléchissants. Si l'on appelle
si les miroirs sont assez réfléchissants. Si l'on appelle
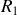 et
et
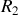 les coefficients de réflexion en intensité sur chaque les deux miroirs de la cavité et si l'on coupe de manière très rapide le faisceau, on constate que le rayonnement persiste dans la cavité. On a en effet :
les coefficients de réflexion en intensité sur chaque les deux miroirs de la cavité et si l'on coupe de manière très rapide le faisceau, on constate que le rayonnement persiste dans la cavité. On a en effet :
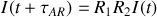
ce qui conduit à
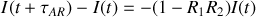
Il s'ensuit que l'intensité décroît dans la cavité comme
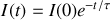
avec
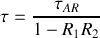
Remarque :
Pour que la durée de vie soit longue il faut donc avoir des miroirs bien réfléchissants.
Supposons que l'on considère une cavité de
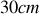 et des miroirs tels que
et des miroirs tels que
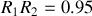 , on a alors
, on a alors
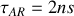 et
et
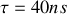 .
.
Modes propres d'une cavité laser
Les modes propres de la cavité laser sont obtenus en considérant que le champ électrique doit s'annuler sur les miroirs du
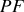 . Si la longueur d'onde d'émission est notée
. Si la longueur d'onde d'émission est notée
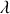 il faut que la distance
il faut que la distance
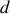 entre les deux miroirs vérifie
entre les deux miroirs vérifie
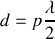
pour que la cavité puisse rentrer en résonance. Si cette condition est vérifiée les ondes se réfléchissent en phase sur chaque miroir. Les modes possibles
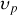 doivent donc satisfaire la relation
doivent donc satisfaire la relation
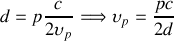
Nous avons vu précédemment que la différence de fréquence entre 2 modes constitue l'
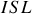 de la cavité. La largeur d'un mode dépend de la finesse et est donnée par
de la cavité. La largeur d'un mode dépend de la finesse et est donnée par
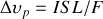 .
.
A cause de l'agitation thermique les niveaux électroniques fluctuent et la fréquence d'émission n'est pas une distribution de Dirac mais une gaussienne centrée sur une fréquence
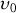 et de largeur spectrale
et de largeur spectrale
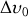 . Cette largeur est très supérieure à celle d'un mode de la cavité.
. Cette largeur est très supérieure à celle d'un mode de la cavité.
Exemple :
nous considérons les modes d'une diode laser
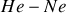 . Cette diode laser émet une radiation de longueur d'onde
. Cette diode laser émet une radiation de longueur d'onde
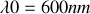 avec une largeur spectrale
avec une largeur spectrale
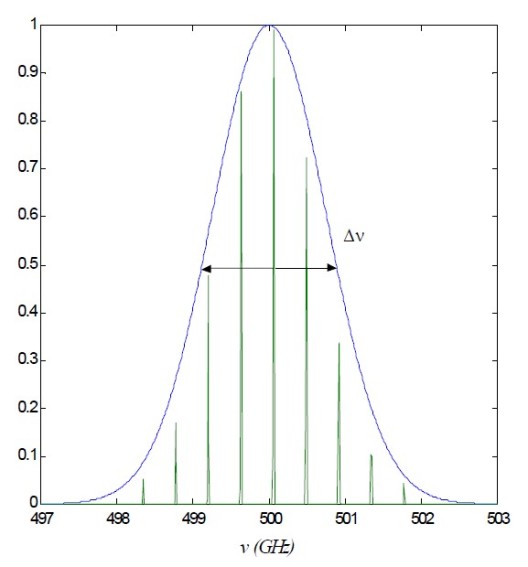
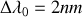 (pleine largeur à mi-hauteur). En fréquence ces données correspondent à
(pleine largeur à mi-hauteur). En fréquence ces données correspondent à
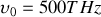 et
et
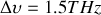 comme le montre la figure 47. Si le laser est formé de miroirs distants de
comme le montre la figure 47. Si le laser est formé de miroirs distants de
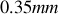 , l'
, l'
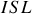 est égal à
est égal à
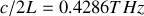 . En supposant que les modes ne peuvent être accrochés que si leur intensité est supérieure à
. En supposant que les modes ne peuvent être accrochés que si leur intensité est supérieure à
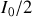 on voit que l'on dispose dans la cavité de
on voit que l'on dispose dans la cavité de
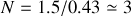 modes. Ces trois modes correspondent à
modes. Ces trois modes correspondent à
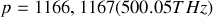 et
et
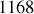 .
.