Il est facile de voir que l'intensité s'écrit
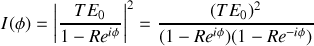
soit

Pour des raisons pratiques il est utile de récrire l'intensité comme

Lorsque
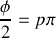 l'intensité est maximale et vaut alors
l'intensité est maximale et vaut alors
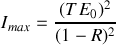
Il s'ensuit que

où l'on a introduit le coefficient
 . La fonction
. La fonction
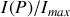 qui est égale à
qui est égale à

s'appelle fonction d'Airy (à ne pas confondre avec la tâche d'Airy).
Nous rappelons qu'en incidence normale les coefficients de Fresnel pour le dioptre 1,0 sont
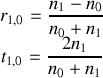
Pour le dioptre verre-air
 et le coefficient
et le coefficient
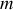 est égal à
est égal à

La figure 41 représente l'évolution de
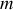 en fonction du coefficient de réflexion du dioptre. Il est évident sur cette figure que
en fonction du coefficient de réflexion du dioptre. Il est évident sur cette figure que
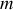 est d'autant plus grand que le coefficient de réflexion est élevé.
est d'autant plus grand que le coefficient de réflexion est élevé.
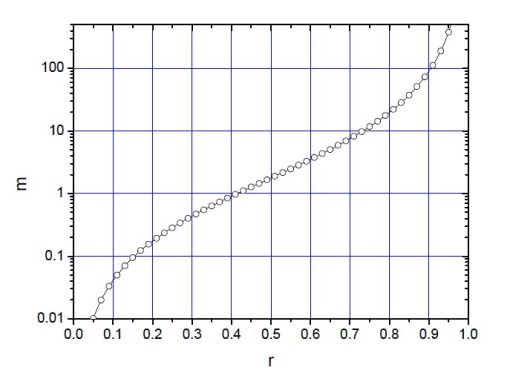
Etude de la fonction d'Airy
Il est facile de voir que la fonction d'Airy est
maximale quand
 et vaut
et vaut
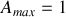
minimale quand
 et vaut
et vaut
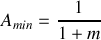
périodique de période

Rappel :
la période de la fonction d'Airy est liée au déphasage
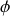 entre les ondes multiples qui sont transmises dans la lame. Le déphasage égal à
entre les ondes multiples qui sont transmises dans la lame. Le déphasage égal à
 peut varier si l'on modifie l'épaisseur
peut varier si l'on modifie l'épaisseur
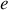 de la lame ou si l'on y transmet une radiation polychromatique.
de la lame ou si l'on y transmet une radiation polychromatique.
D'autre part la fonction d'Airy est d'autant plus contrastée que le valeur de
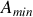 sera petite. Le contraste est défini par
sera petite. Le contraste est défini par
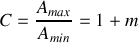
L'étude de la fonction peut donc être limitée à l'intervalle
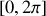 et l'intensité maximale peut être étudiée au voisinage de
et l'intensité maximale peut être étudiée au voisinage de
 ce qui correspond à
ce qui correspond à

La fonction
 est une Lorentzienne. Sa pleine largeur à mi-hauteur
est une Lorentzienne. Sa pleine largeur à mi-hauteur
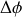 qui correspond à
qui correspond à
 est donnée par
est donnée par

Le rapport de la période de la fonction d'Airy à la pleine largeur à mi-hauteur s'appelle finesse,
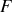 , et vaut
, et vaut
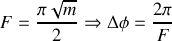
Il s'ensuit que les maxima seront d'autant plus fins que
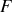 sera grand. Nous présentons sur la figure 42 un exemple de l'influence de la finesse sur la fonction d'Airy. Nous observons très clairement que le contraste est d'autant plus faible que la finesse est petite. Pour
sera grand. Nous présentons sur la figure 42 un exemple de l'influence de la finesse sur la fonction d'Airy. Nous observons très clairement que le contraste est d'autant plus faible que la finesse est petite. Pour
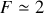 , la réponse de la cavité est quasi sinusoïdale et l'on peut considérer que l'on a interférence à deux ondes. Plus le coefficient de réflexion augmente et plus le nombre d'ondes qui interfèrent est grand. Empiriquement on admet parfois que la finesse représente le nombre de rayons qui interfèrent ; ainsi pour une finesse de 10 on admettra que 10 rayons interfèrent.
, la réponse de la cavité est quasi sinusoïdale et l'on peut considérer que l'on a interférence à deux ondes. Plus le coefficient de réflexion augmente et plus le nombre d'ondes qui interfèrent est grand. Empiriquement on admet parfois que la finesse représente le nombre de rayons qui interfèrent ; ainsi pour une finesse de 10 on admettra que 10 rayons interfèrent.

Il importe de remarquer que nous venons de faire l'étude de la fonction d'Airy en fonction du déphasage
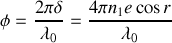 . Si l'on considère une cavité d'indice
. Si l'on considère une cavité d'indice
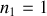 et d'épaisseur
et d'épaisseur
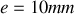 éclairée en incidence normale par une radiation monochromatique de longueur d'onde
éclairée en incidence normale par une radiation monochromatique de longueur d'onde
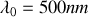 , le déphasage au centre de la cavité est donnée par
, le déphasage au centre de la cavité est donnée par

On voit ainsi que l'ordre au centre est gigantesque et vaut
 . Cet ordre étant entier il y aura un maximum d'intensité au centre de la cavité. L'ordre 19999 sera l'ordre correspondant au maximum suivant et sera observé à un angle
. Cet ordre étant entier il y aura un maximum d'intensité au centre de la cavité. L'ordre 19999 sera l'ordre correspondant au maximum suivant et sera observé à un angle
 correpondant à
correpondant à
 . La fonction est caractérisée par une série de dents qui deviennent très pointues quand la finesse est élevée. Elle tend vers un peigne de Dirac pour une finesse de l'ordre de 100. On voit également que la cavité produit un maximum d'intensité en son centre si et seulement si l'épaisseur de la cavité vérifie
. La fonction est caractérisée par une série de dents qui deviennent très pointues quand la finesse est élevée. Elle tend vers un peigne de Dirac pour une finesse de l'ordre de 100. On voit également que la cavité produit un maximum d'intensité en son centre si et seulement si l'épaisseur de la cavité vérifie
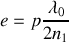
Dans l'air
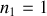 et il faut donc que l'épaisseur de la cavité soit une multiple entier de demi longueur d'onde pour produire un maximum en son centre. Cette condition est l'équivalent d'une condition de résonance que l'on retrouve par exemple dans le cas d'une corde vibrante. Cette condition est difficile à réaliser car elle doit être satisfaite à mieux que
et il faut donc que l'épaisseur de la cavité soit une multiple entier de demi longueur d'onde pour produire un maximum en son centre. Cette condition est l'équivalent d'une condition de résonance que l'on retrouve par exemple dans le cas d'une corde vibrante. Cette condition est difficile à réaliser car elle doit être satisfaite à mieux que
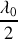
Si au lieu de travailler à longueur d'onde fixe on envoie dans la cavité une radiation polychromatique on a alors
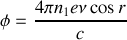
On constate que le déphasage est proportionnel à la fréquence
 de l'onde ce qui permet d'affirmer que la fonction d'Airy présentera des maximas à des fréquences particulières. La distance entre deux dents consécutives du peigne est égale à
de l'onde ce qui permet d'affirmer que la fonction d'Airy présentera des maximas à des fréquences particulières. La distance entre deux dents consécutives du peigne est égale à
 si l'on travaille en phase. A une variation de phase de
si l'on travaille en phase. A une variation de phase de
 engendrée par le passage de l'ordre
engendrée par le passage de l'ordre
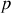 à
à
 , correspond une variation de fréquence
, correspond une variation de fréquence
 . Cette différence appelée intervalle spectral libre (ISL) est égale en incidence normale pour une lame d'air à
. Cette différence appelée intervalle spectral libre (ISL) est égale en incidence normale pour une lame d'air à
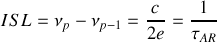
ou
 désigne le temps mis par un rayon lumineux pour faire un aller-retour dans la cavité. L'ISL pour une cavité remplie d'air ne dépend donc que de l'épaisseur de la cavité.
désigne le temps mis par un rayon lumineux pour faire un aller-retour dans la cavité. L'ISL pour une cavité remplie d'air ne dépend donc que de l'épaisseur de la cavité.
La finesse s'écrit également
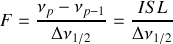
Données numériques
Supposons que la cavité soit de l'air enfermé entre deux parois de verre revêtues de couches diélectriques assurant un coefficient de réflexion de 0.96 séparées d'une distance
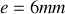 . On a alors
. On a alors

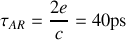
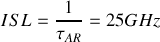
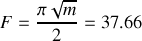
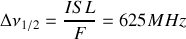
Si l'on considère une radiation de longueur d'onde de centrage
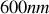 entrant dans la cavité on voit que
entrant dans la cavité on voit que
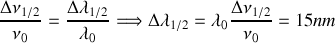
Calcul du rayon des anneaux
Nous notons que les anneaux brillants correspondent à un déphasage multiple de
 ce qui donne leur ordre d'interférence
ce qui donne leur ordre d'interférence
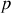
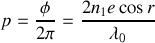 avec
avec
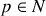
L'ordre d'interférence est demi-entier pour les anneaux sombres.
D'une façon générale pour un angle
 on peut calculer un ordre
on peut calculer un ordre
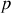 quelconque (fractionnaire) qui vérifie
quelconque (fractionnaire) qui vérifie
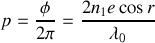
Le rayon des anneaux dépend évidemment de leur ordre. A l'ordre
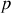 , on a donc
, on a donc
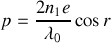
Le calcul très semblable à celui effectué pour une couche mince en réflexion montre que :
au centre
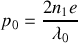
le premier anneau brillant se trouve à l'ordre


A l'ordre
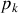 qui correspond à l'anneau brillant
qui correspond à l'anneau brillant
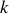 on a donc
on a donc

ce qui conduit à
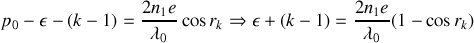
Si l'on fait l'hypothèse que le rayon angulaire des anneaux est petit alors
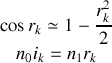
Il s'ensuit que le rayon angulaire
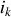 de réflexion de l'anneau brillant numéro
de réflexion de l'anneau brillant numéro
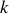 est donné par
est donné par

Le rayon angulaire d'un anneau sombre suit évidemment la même loi, mais il diffère de celui de l'anneau brillant d'une valeur 1/2 qui peut être incluse dans l'ordre fractionnaire
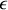 . Du point de vue expérimental il convient de remarquer que la mesure effectuée est toujours celle du rayon de l'anneau et non celle du rayon angulaire. Pour cela on utilise une lentille de grande focale
. Du point de vue expérimental il convient de remarquer que la mesure effectuée est toujours celle du rayon de l'anneau et non celle du rayon angulaire. Pour cela on utilise une lentille de grande focale
 ou un viseur réglé par autocollimation sur l'infini. Comme le rayon angulaire des anneaux est faible nous pouvons assimiler l'angle de réflexion à sa tangente et comme l'indique la figure il est facile de voir que
ou un viseur réglé par autocollimation sur l'infini. Comme le rayon angulaire des anneaux est faible nous pouvons assimiler l'angle de réflexion à sa tangente et comme l'indique la figure il est facile de voir que





