En particulier, si deux radiations très voisines l'une de l'autre sont présentes dans le spectre nous aurons pour le même ordre

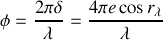
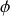Toute variation de la longueur d'onde engendrera à donné une variation de phase donnée par la différentielle de 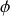soit

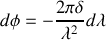
Si nous repérons cette variation au voisinage d'un anneau brillant nous avons 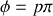, ce qui se traduit par

Si l'on applique le critère de Rayleigh qui veut que deux radiations soient séparables si le maximum de l'une est au moins séparé du maximum de l'autre de la demi-largeur à mi-hauteur du maximum il vient

(7)

Par définition la quantité définit le pouvoir de résolution du Pérot-Fabry. La relation (7) montre que pour augmenter le pouvoir de résolution il importe soit de regarder à ordre élevé, donc près du centre, soit d'augmenter la finesse, c'est à dire le coefficient de réflexion du dioptre air-verre. A titre d'exemple nous considérons un d'épaisseur 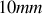éclairé avec une radiation de longueur d'onde 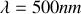. L'ordre au centre est donc 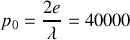. En supposant une finesse de 30 ce qui est raisonnable nous voyons que le pouvoir de résolution atteint 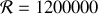. Un tel appareil permet en théorie de résoudre 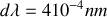ce qui est évidemment remarquable.

On conçoit que si l'on interpose un trou au centre de la figure d'interférences d'un , il soit possible de ne laisser passer que l'ordre au centre. Si celui-ci est un entier, un anneau brillant est transmis dans le trou avec une résolution en longueur d'onde fantastique.