On a montré précédemment que l'énergie interne et l'enthalpie était des potentiels pour le travail adiabatique. Les potentiels
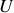et
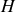sont donc adaptés à l'étude de systèmes thermiquement isolés. Il existe d'autres cas de figure importants dans la nature, pour lesquels ces deux fonctions sont moins intéressantes. Considérons en particulier la situation où le système
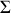étudié est en contact avec un thermostat
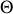. Deux situations idéales peuvent être considérées, selon que le volume du système
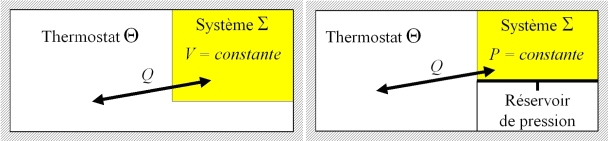
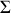est constant ou que sa pression est maintenue constante. Elles sont représentées par la figure 4. L'ensemble
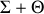étant isolé, toute évolution du système
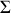vers son état d'équilibre s'accompagne d'une augmentation de l'entropie de l'Univers :
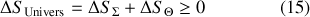
Or, la variation d'entropie du thermostat
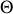se résume au rapport
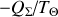. Par suite,
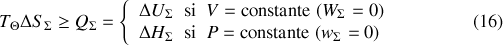
Toute transformation monotherme d'un système
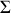s'accompagne donc des inégalités :
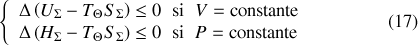
Dans l'hypothèse où le système
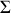est à la température du thermostat
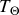en son état initial et en son état final, cela conduit à l'important résultat (18).
Toute évolution spontanée vers un état d'équilibre d'un système en contact avec un thermostat (transformation monotherme) s'accompagne d'une diminution de l'énergie libre
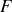(à volume constant) ou de l'enthalpie libre
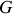(à pression constante).
Les fonctions
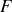et
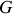sont donc minimales à l'équilibre (
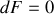et
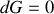). Cette autre expression du principe d'évolution qu'est le second principe montre que
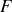et
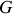sont des potentiels adaptés à l'étude de systèmes en contact avec une source thermique. En particulier,
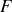et
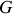sont des potentiels pour le travail des transformations monothermes (en contact avec un thermostat). Pour le montrer, considérons tout d'abord le cas idéal d'une transformation quasi-statique isotherme et donc réversible :
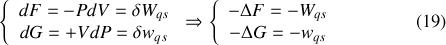
Dans le cas monotherme, pas nécessairement isotherme quasi-statique, l'inégalité (7) entraîne :
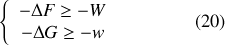
Les travaux
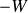et
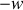étant ceux échangés par l'opérateur, les quantités
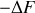et
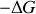sont les quantités de travail que l'opérateur récupère ou dépense dans la configuration optimale d'une transformation monotherme (c'est à dire dans le cas de l'isotherme réversible).
Remarque :
C'est dans ce dernier résultat que l'origine du qualificatif « libre »
attribué aux potentiels
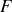et
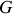doit être comprise. Le travail est en effet ce qui intéresse l'opérateur utilisant une machine thermique. Cette énergie peut être utilisée en mécanique (force motrice) comme en thermique (chauffage). A contrario, l'énergie thermique, si elle peut bien sûr avoir une utilisation thermique, ne peut être intégralement convertie en travail (second principe). En ce sens elle est une quantité d'énergie « liée »
. Si on assimile cette énergie liée au produit
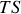, il apparaît que
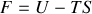et
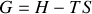sont libres parce qu'on leur a soustrait la partie liée.
