Les capacités thermiques absolues 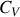et et 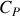les coefficients thermiques 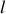et 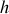d'un système sont définis par la relation du transfert thermique quasi-statique à la variation d'entropie :

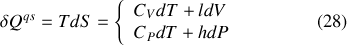
Des différentielles (1) et des relations de Gibbs-Helmholtz, il est donc loisible de déduire des relations entre capacités thermiques et potentiels thermodynamiques :

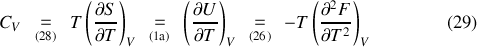
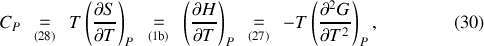
tandis que l'utilisation des relations de Maxwell (23) et (24) permet de retrouver les « relations de Clapeyron » définissant les coefficients thermiques 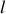et en fonction de dérivées partielles du volume ou de la pression :

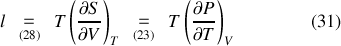
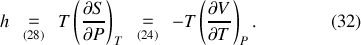
L'entropie étant une dérivée partielle de l'énergie libre 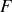comme de l'enthalpie libre 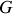, il est également possible de définir les coefficients thermiques 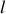et 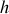en fonction de la dérivée seconde, mixte dans ce cas, d'un potentiel libre :

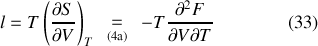
Enfin, les coefficients thermoélastiques 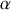(dilatation isochore), 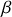(dilatation isobare) et 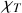(compressibilité isotherme) apparaissent eux aussi susceptibles d'être exprimés en fonction des dérivées secondes de 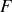et :

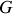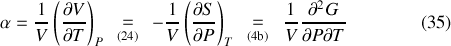
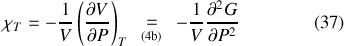
Le coefficient de compressibilité isentropique dérive quant à lui de l'enthalpie :

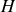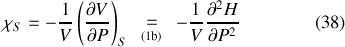
Ce sont donc tous les coefficients thermiques utiles à l'étude des systèmes qui dérivent des potentiels thermodynamiques, c'est à dire des deux concepts centraux que sont l'énergie et l'entropie.