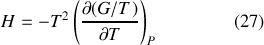Les expressions différentielles (1) et (4) sont celles de fonctions d'état. À ce titre, les dérivées partielles qui y interviennent doivent vérifier la condition de Schwarz (égalité des dérivées secondes mixtes). Les « Relations de Maxwell »
explicitent cette condition :

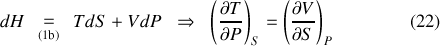
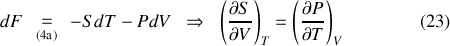
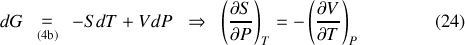
Loin d'être de simples jeux d'écriture mathématique, ces équations mettent en relation des transformations du système de natures différentes et possèdent une valeur prédictive. La relation de Maxwell (21), par exemple, compare les dérivées associées à une isentropique et à une isochore. La variation de pression accompagnant un transfert thermique à volume constant peut être directement extrapolée de celle de la température en fonction du volume au cours d'une adiabatique quasi-statique. Relevons enfin que les expressions (4) permettent aussi de montrer que l'énergie interne et l'enthalpie dérivent de l'énergie libre et de l'enthalpie libre. En effet, et alors qu'un résultat similaire peut être obtenu en substituant
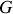 à
à
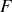 et
et
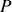 à
à
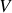 ,
,
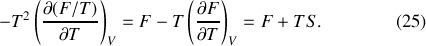
On en déduit les deux « Relations de Gibbs-Helmholtz »
: