On présente ici une modélisation théorique algébriquement plus simple , que celle de Rutherford, pour dériver sa formule de la section efficace de diffusion de particules alpha positivement chargées par un noyau également positivement chargé.

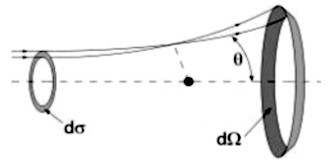
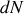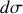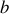Considérons que les particules alpha sont incidentes de la gauche sur un noyau schématisé comme le cercle noir dans la Fig. 8. Considérons particules alpha qui traversent un anneau dont et 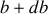, sont les rayons interne et externe, (voir l'anneau dans la figure). Ces 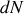particules traversent l'aire d'anneau. Si 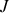est le flux de particules incidentes par unité de surface par unité du temps, on a :

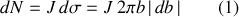
Ces mêmes 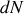particules sont diffusées dans un angle solide 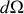où :

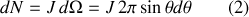
Notons que les particules incidentes à la distance 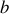de l'axe central, (le rayon intérieure de l'anneau), sont diffusées dans un angle légèrement plus important 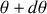que l'angle 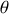dans lequel diffusent les particules incidentes à 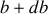(le rayon extérieure de l'anneau). Ceci est bien normal vu la nature de la force de répulsion entre l'alpha et le noyau ; plus l'alpha se rapproche du noyau, plus elle serait diffusée par la force de répulsion.

figure 8 : Un schéma illustrant les trajets de diffusion de la particule alpha par un noyau

La particule alpha porte la charge 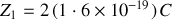; posons que le noyau porte une charge 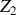à préciser éventuellement pour chaque élément. La force de répulsion colombienne 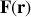s'écrit comme :

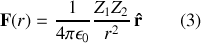
Notons que représente la distance entre le noyau et la particule alpha, si bien que 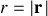, où 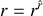le vecteur de position de la particule alpha par rapport au noyau (pris comme l'origine d'un repère cartésien). Cette distance 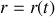varie naturellement avec le temps 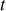, lors du processus de diffusion.

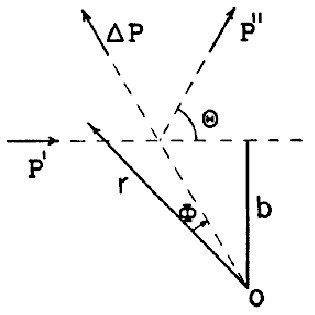
On va analyser ensuite la diffusion grâce aux lois de conservation de l'énergie et de la quantité de mouvement pour la particule alpha. La Fig. 9 présente ainsi les différentes quantités d'intérêt. Notons que 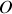décrit la position du noyau à l'origine du repère.

figure : 9 Un schéma décrivant la conservation de la quantité de mouvement pour la diffusion de la particule alpha par un noyau.

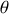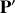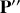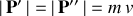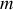Considérons comme l'angle final de la déviation du trajet d'une particule alpha lors de son interaction avec le noyau. et sont les vecteurs de quantités de mouvement initiale et finale de cette particule et puisqu'il n y a pas de perte d'énergie on peut écrire où et 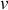sont la masse et la vitesse, respectivement, de l'alpha. Sur la Fig. 9, 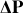est le changement total du vecteur de la quantité de mouvement 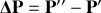suite à la diffusion. On peut démontrer par la géométrie de la figure, que :

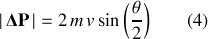
Prenons ensuite 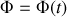comme l'angle, (variable avec le temps), entre le vecteur et le vecteur 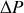. Le théorème de conservation de la quantité de mouvement et de l'impulsion peut s'écrire comme :

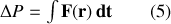
Combinant les équations (4) et (5), afin de sommer dans le temps les contributions des impulsions lors du processus de diffusion, on a :

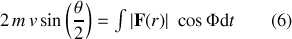
Considérons ensuite la variation du mouvement angulaire dans le plan décrit par les coordonnées polaires ( 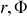). Cela peut s'écrire par la relation :

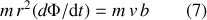
La quantité 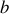, qui correspond au rayon intérieure de l'anneau dans la Fig. 8, s'appelle dorénavant le paramètre d'impact. En multipliant l'équation (6) par 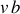et en utilisant l'équation (7), on obtient la relation :

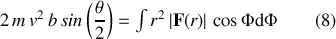
En remplaçant les variations du temps 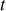par les variations de l'angle , où on peut vérifier que les limites inférieure et supérieure de l'intégration deviennent respectivemen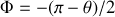t et 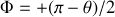, pour la force colombienne de répulsion.

Avec un changement de variable de 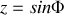, on peut écrire encore que :

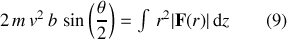
où les limites inférieure et supérieure de l'intégration deviennen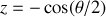t et .

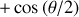Vu que 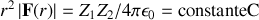pour un élément donné, par l'équation (3), on peut intégrer directement l'équation (9) et démontrer une relation unique entre le paramètre d'impact 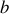et l'angle de déviation, 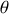, à savoir :

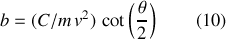
La relation (10) permet enfin de dériver la formule de la section efficace de diffusion de Rutherford pour les particules alpha (et pour d'autres particules chargées), en utilisant les équations (1) et (2)

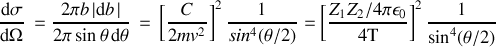
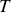est l'énergie cinétique de la particule alpha. La section efficace varie donc inversement avec 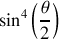et 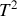. La constante 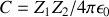dépend de la charge 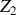portée par le noyau cible bombardé.

figure 10 : L'accord entre des résultats expérimentaux de Geiger et al. (cercles ouverte) et la formule théorique de Rutherford (courbe continue) pour la diffusion de particules alpha.

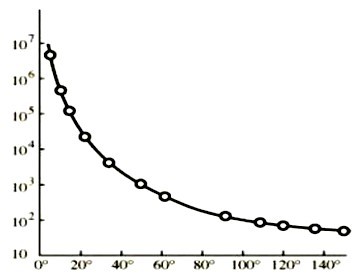
La Fig. 10 présente une comparaison entre les résultats expérimentaux de Geiger et son étudiant Marsden (cercles ouverts, pour des petits angles allant jusqu'à 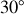), et la formule théorique de Rutherford pour la section efficace de diffusion de particules alpha.