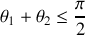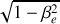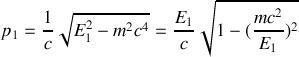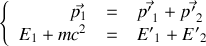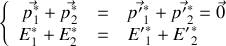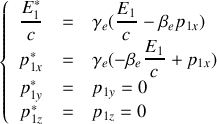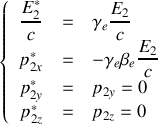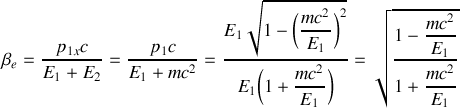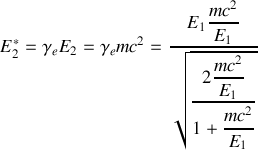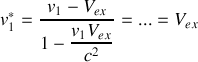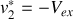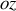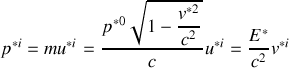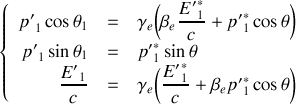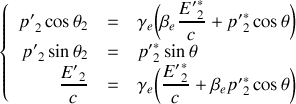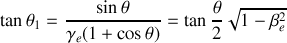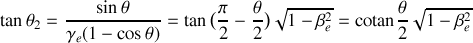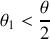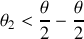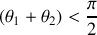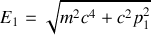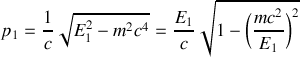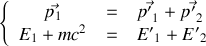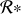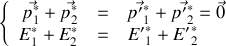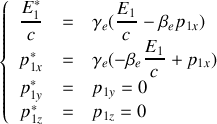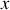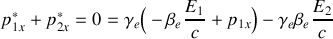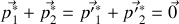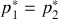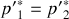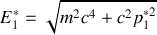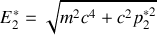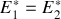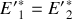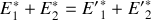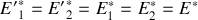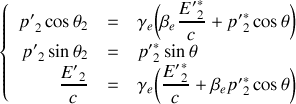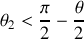Énoncé
On considère la collision élastique de deux protons de masse m, le premier ayant une vitesse
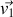et le second étant au repos, dans le référentiel inertiel
:
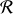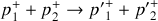
1. Montrer que
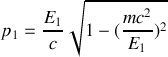et que
.
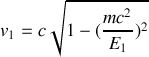2. Écrire les équations de conservation de l'énergie et de la quantité de mouvement dans le référentiel
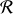et dans le référentiel barycentrique
.
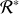On s'intéresse aux particules avant le choc.
3. Appliquer les transformations de Lorentz au quadrivecteur énergie-impulsion pour exprimer
,
,
,
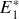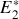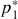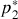en fonction de
,
,
,
.
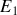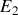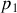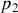4. Montrer que la vitesse
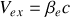de
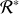par rapport à
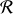est telle que
.
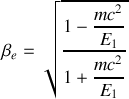5. Exprimer
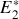en fonction de
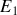et de
.
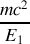6. Déterminer dans
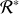la vitesse de chaque proton avant le choc.
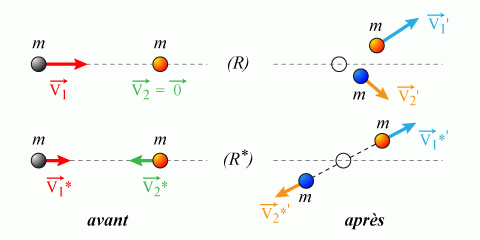
On s'intéresse ensuite aux particules après le choc. Dans
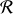, le proton incident est dévié d'un angle
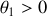et le proton au repose recule d'un angle
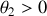par rapport à la direction du proton incident. Dans
le proton incident se déplace après la collision d'un angle
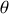par rapport à la direction initiale.
7. Faire un schéma de la situation avant et après le choc, dans les deux référentiels.
8. Montrer que
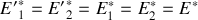. En déduire que
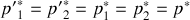et que
.
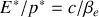9. Relier les expressions dans
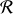du quadrivecteur énergie-impulsion de chacun deux protons avec celles correspondantes dans
.
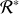10. Montrer que
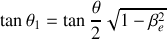et que
.
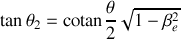11. Montrer que
