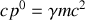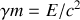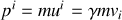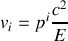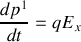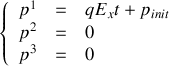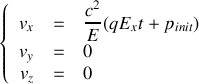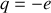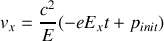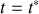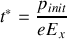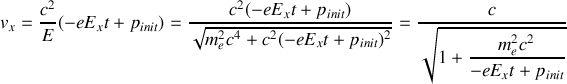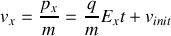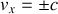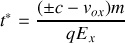Énoncé
Pour exploiter le système d'équations différentielles associées à la force de Lorentz,
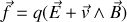
il est d'usage, en relativité, d'utiliser la relation (
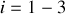 ) :
) :
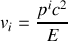
1. Démontrer cette dernière relation, où
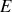 est l'énergie de la particule (à ne pas confondre avec
est l'énergie de la particule (à ne pas confondre avec
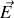 ).
).
Un électron, dont la quantité de mouvement initiale
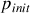 est non-nulle selon
est non-nulle selon
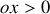 , est soumis à l'action d'un champ électrique, orienté lui aussi selon
, est soumis à l'action d'un champ électrique, orienté lui aussi selon
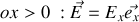 .
.
2. En utilisant la force de Lorentz, obtenir l'expression des composantes
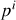 .
.
3. Détailler les composantes
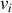 .
.
4. La charge de l'électron étant négative, au bout de quelle durée
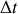 l'électron s'arrête-t-il?
l'électron s'arrête-t-il?
5. L'électron repart ensuite dans la direction
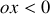 . Quelle vitesse atteint-il lorsque
. Quelle vitesse atteint-il lorsque
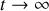 (justifier)? Ce résultat est-il compatible avec les postulats d'Einstein?
(justifier)? Ce résultat est-il compatible avec les postulats d'Einstein?
6. Reprendre le problème dans le cas classique. Montrer que la vitesse de l'électron vaudra
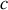 après une durée à déterminer, et puis dépassera cette valeur.
après une durée à déterminer, et puis dépassera cette valeur.