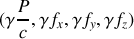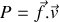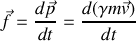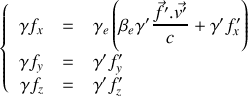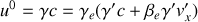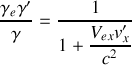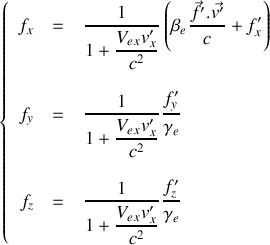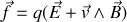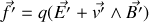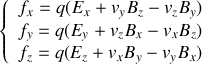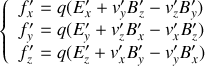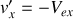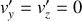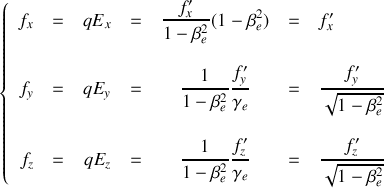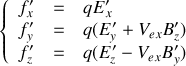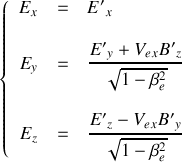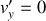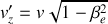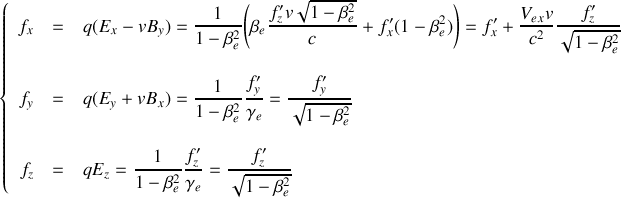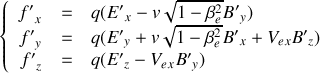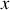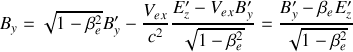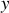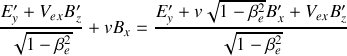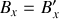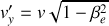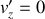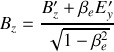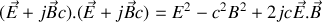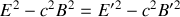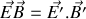Énoncé
On considère une particule ponctuelle de masse
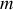 et de vitesse
et de vitesse
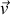 dans le référentiel inertiel
dans le référentiel inertiel
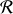 qui possède une charge électrique
qui possède une charge électrique
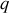 . Elle est soumise à un champ électromagnétique caractérisé par les vecteurs électrique
. Elle est soumise à un champ électromagnétique caractérisé par les vecteurs électrique
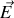 et magnétique
et magnétique
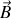 qui satisfont la relation de la force de Lorentz.
qui satisfont la relation de la force de Lorentz.
Montrer que les formules de transformation d'une force
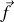 agissant sur une particule de vitesse
agissant sur une particule de vitesse
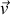 dans
dans
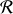 et
et
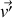 dans
dans
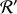 s'écrivent :
s'écrivent :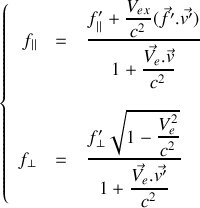
Pour cela, on appliquera les transformations de Lorentz au quadrivecteur force et on utilisera la formule de transformation des vitesses, pour la composante
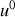 .
.On considère trois cas particuliers, à savoir la particule chargée a soit une vitesse nulle soit une vitesse dirigée selon
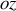 , soit une vitesse dirigée selon
, soit une vitesse dirigée selon
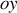 dans
dans
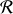 . Obtenir les formules qui relient les composantes des champs électrique et magnétique dans
. Obtenir les formules qui relient les composantes des champs électrique et magnétique dans
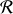 et dans
et dans
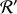 . Sans le démontrer, on peut dire que ces formules restent valables dans le cas d'une vitesse
. Sans le démontrer, on peut dire que ces formules restent valables dans le cas d'une vitesse
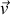 quelconque.
quelconque.Montrer que le carré scalaire du vecteur complexe
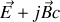 est invariant par changement de référentiel inertiel.
est invariant par changement de référentiel inertiel.