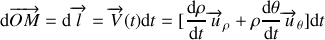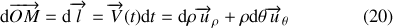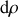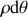Dérivation du vecteur position et vitesse angulaire
La base
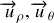 est constituée de vecteurs « mobiles » dans le repère : ces vecteurs changent de direction au cours du temps. En utilisant l'expression (2) du vecteur position en coordonnées polaires et les règles de dérivation d'un produit de fonctions, on a :
est constituée de vecteurs « mobiles » dans le repère : ces vecteurs changent de direction au cours du temps. En utilisant l'expression (2) du vecteur position en coordonnées polaires et les règles de dérivation d'un produit de fonctions, on a :
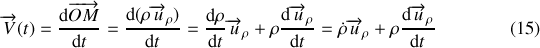
D'après l'expression (3c) le vecteur
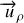 apparaît comme une fonction de la coordonnée angulaire
apparaît comme une fonction de la coordonnée angulaire
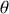 elle-même fonction du temps au cours du mouvement du point
elle-même fonction du temps au cours du mouvement du point
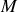 . La dérivation d'une fonction composée permet d'écrire :
. La dérivation d'une fonction composée permet d'écrire :
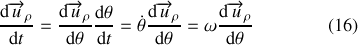
La quantité
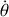 caractérise la variation de l'angle polaire au cours du temps et correspond à la définition de la vitesse angulaire. Elle est souvent notée
caractérise la variation de l'angle polaire au cours du temps et correspond à la définition de la vitesse angulaire. Elle est souvent notée
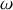 (lettre grecque oméga) et s'exprime en radian/seconde
(lettre grecque oméga) et s'exprime en radian/seconde
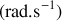 .
.
Dérivation par rapport à l'angle θ d'un vecteur tournant de norme constante
L'application des règles de dérivation sur l'expression (3c) du vecteur
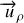 donne :
donne :
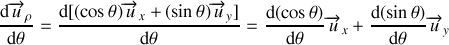
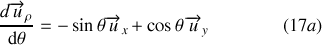
D'après la relation (3d) on obtient finalement :
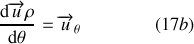
De même pour le vecteur
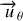 :
:
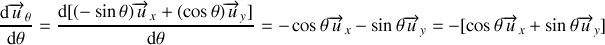
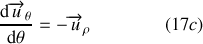
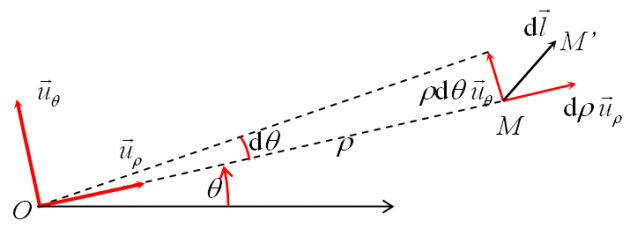
Règle de dérivation d'un vecteur unitaire par rapport à l'angle polaire :
La dérivée par rapport à l'angle polaire
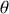 d'un vecteur unitaire
d'un vecteur unitaire
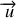 (qui ne dépend que de l'angle
(qui ne dépend que de l'angle
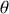 ) est un vecteur unitaire qui lui est directement perpendiculaire (rotation de
) est un vecteur unitaire qui lui est directement perpendiculaire (rotation de
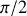 dans le sens positif).
dans le sens positif).
Dérivation par rapport au temps d'un vecteur tournant de norme constante
D'après la relation (16) on a :
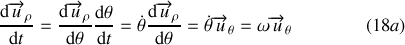
De même :
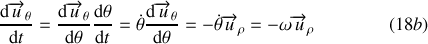
Règle de dérivation d'un vecteur unitaire par rapport au temps :
La dérivée par rapport au temps
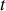 d'un vecteur
d'un vecteur
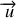 de norme constante est un vecteur dont la norme est obtenue en multipliant celle de
de norme constante est un vecteur dont la norme est obtenue en multipliant celle de
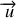 par la vitesse angulaire
par la vitesse angulaire
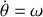 et qui est directement perpendiculaire à
et qui est directement perpendiculaire à
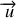 (rotation de
(rotation de
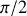 dans le sens positif).
dans le sens positif).
Expression du vecteur vitesse en coordonnées polaires
En reprenant l'expression (15) et en utilisant le résultat (18a) on a :
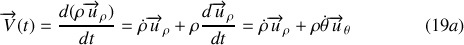
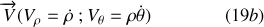
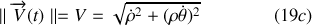
Les grandeurs
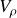 et
et
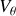 sont respectivement les composantes radiale et orthoradiale du vecteur vitesse dans la base polaire.
sont respectivement les composantes radiale et orthoradiale du vecteur vitesse dans la base polaire.