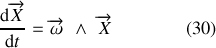Définition
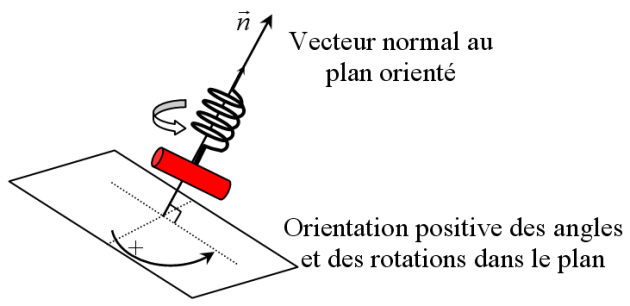
Nous avons vu que la base polaire
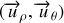 est une base mobile. Les vecteurs de cette base tourne autour de l'axe
est une base mobile. Les vecteurs de cette base tourne autour de l'axe
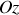 avec une vitesse angulaire
avec une vitesse angulaire
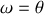 . Pour caractériser cette rotation il suffit de se donner la valeur de la vitesse angulaire et la direction autour de laquelle les vecteurs tournent. Il est donc pratique d'introduire un vecteur vitesse angulaire
. Pour caractériser cette rotation il suffit de se donner la valeur de la vitesse angulaire et la direction autour de laquelle les vecteurs tournent. Il est donc pratique d'introduire un vecteur vitesse angulaire
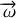 dont la direction est celle de l'axe de rotation et le module la valeur de la vitesse angulaire. Le sens de ce vecteur oriente automatiquement les rotations dans le plan par la règle habituelle du tire-bouchon (voir figure 12).
dont la direction est celle de l'axe de rotation et le module la valeur de la vitesse angulaire. Le sens de ce vecteur oriente automatiquement les rotations dans le plan par la règle habituelle du tire-bouchon (voir figure 12).
Le vecteur vitesse angulaire caractérisant la rotation des vecteurs de la base polaire est donc un vecteur suivant l'axe
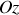 et de module correspondant à la valeur algébrique de la vitesse angulaire
et de module correspondant à la valeur algébrique de la vitesse angulaire
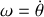 (une valeur positive donne une rotation dans le sens positif).
(une valeur positive donne une rotation dans le sens positif).
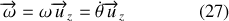
Attention :
Le vecteur vitesse
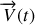 d'un point
d'un point
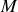 se déplaçant dans le plan
se déplaçant dans le plan
 est un vecteur dans ce plan alors que le vecteur vitesse angulaire
est un vecteur dans ce plan alors que le vecteur vitesse angulaire
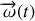 est un vecteur perpendiculaire à ce plan. Bien faire la distinction entre ces deux grandeurs.
est un vecteur perpendiculaire à ce plan. Bien faire la distinction entre ces deux grandeurs.
Dérivée des vecteurs de la base polaire en fonction du vecteur vitesse angulaire
La dérivée du vecteur
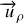 est donné par l'expression (18a) :
est donné par l'expression (18a) :
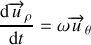
La base
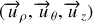 des coordonnées cylindriques est une base orthonormée directe. Cela signifie qu'il est toujours possible d'exprimer l'un de ces vecteurs par un produit vectoriel des deux autres en respectant l'ordre. On a par exemple :
des coordonnées cylindriques est une base orthonormée directe. Cela signifie qu'il est toujours possible d'exprimer l'un de ces vecteurs par un produit vectoriel des deux autres en respectant l'ordre. On a par exemple :
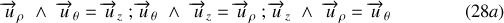
Dans chacun des cas précédents l'ordre
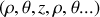 est respecté. Dans le cas contraire il suffit de mettre un signe moins :
est respecté. Dans le cas contraire il suffit de mettre un signe moins :
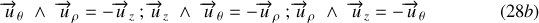
Dans ce cas, l'expression (18a) devient :
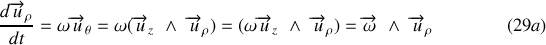
De même :
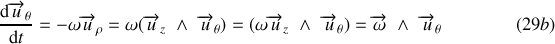
Ce résultat se généralise pour un vecteur
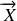 de norme constante (
de norme constante (
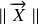 = constante) en rotation caractérisée par le vecteur vitesse angulaire
= constante) en rotation caractérisée par le vecteur vitesse angulaire
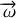 . Ce vecteur est une combinaison linéaire des vecteurs de base et donc on a :
. Ce vecteur est une combinaison linéaire des vecteurs de base et donc on a :