Définition : La transformation de Galilée
Soit le référentiel
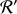animé d'un mouvement rectiligne uniforme, de vitesse
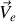par rapport à un système de référence galiléen
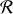, supposé fixe, une particule est respectivement décrite par
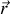et
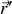dans les référentiels
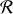et
.
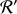Les 2 égalités suivantes :
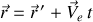
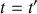
permettent le passage d'un référentiel à l'autre et caractérisent la transformation de Galilée.
En résumé :
Ces deux égalités garantissent l'invariance du principe fondamental de la dynamique dans ces référentiels.
Une infinité de référentiels galiléens existent : toute particule libre, en mouvement rectiligne uniforme, évolue dans un espace homogène et isotrope et est porteuse d'un référentiel galiléen.
