Attention :
Dans ce paragraphe, l'objectif est de donner une réponse à la question :
Que deviennent les éléments cinématiques lorsque l'on change de référentiel galiléen ?
car si les équations du mouvement et le principe fondamental de la dynamique ne sont pas modifiés,
Comment se transforment impulsion et moment cinétique d'un référentiel galiléen à l'autre ?
et dans la généralisation à
 corps :
corps :
Que deviennent-ils pour un système à
 corps ?
corps ?
Quelles propriétés vérifient-ils ?
i. Composition des impulsions
Pour une particule élémentaire de masse
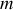 , la composition des vitesses :
, la composition des vitesses :
 permet de déduire la loi de composition des quantités de mouvement
permet de déduire la loi de composition des quantités de mouvement
 .
.
Une première conclusion, obtenue en dérivant par rapport au temps la quantité de mouvement, permet de composer les accélérations.
Le PFD reste inchangé d'un référentiel galiléen à l'autre (
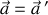 ).
).
La loi physique conserve sa forme la plus simple.
La généralisation à
 points matériels de masses
points matériels de masses
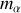 conduit aux impulsions totales :
conduit aux impulsions totales :
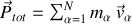 dans
dans
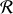 et
et
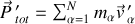 dans
dans
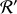 .
.
Ces impulsions vérifient une loi de composition des impulsions selon :

Cette relation permettra de déduire une propriété du centre d'inertie noté G
Rappel : Centre d'inertie, centre de masse, centre de gravité
Le centre de masse est défini par :
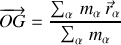
Si les masses sont remplacées par les poids, sa définition ne change pas mais ce point devient le centre de gravité.
Lorsque
 est confondu avec
est confondu avec
 , la définition barycentrique du CDM est obtenue :
, la définition barycentrique du CDM est obtenue :

Fondamental : Propriété du centre d'inertie
D'après la composition des impulsions, le centre d'inertie
 est le centre du référentiel galiléen dans lequel l'impulsion totale est nulle soit :
est le centre du référentiel galiléen dans lequel l'impulsion totale est nulle soit :
 .
.
La vitesse du centre d'inertie est donnée par :
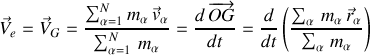
Ce point correspond au centre de masse ou de gravité, définis par le système de points, sa géométrie, ses symétries.
Cette propriété donne un rôle particulier au référentiel de centre
 , en mécanique du solide notamment.
, en mécanique du solide notamment.
ii. Moment cinétique total et choix d'une autre origine des coordonnées
Dans le cas du moment cinétique, ou de moment de force, l'origine du référentiel est essentielle à son évaluation mathématique et au bras de levier constitué avec l'axe de rotation.
Deux cas se présentent : l'origine du référentiel est fixe ou mobile.
Si
 est fixe et
est fixe et
 , tout point
, tout point
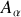 est représenté par son rayon-vecteur,
est représenté par son rayon-vecteur,
 .
. Les relations suivantes
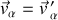 , et
, et
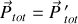 permettent de déduire le moment de la quantité de mouvement totale
permettent de déduire le moment de la quantité de mouvement totale
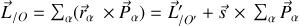
tenant compte des origines
 et
et
 .
.
Le moment cinétique est invariant si
 est nul.
est nul.
Le théorème du moment cinétique évalué respectivement par rapport aux deux points fixes
 et
et
 s'écrit :
s'écrit :
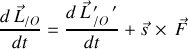
où le PFD a été utilisé.
Le théorème du moment cinétique est invariant si
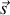 est parallèle à la résultante des forces
est parallèle à la résultante des forces
 .
.
Moment cinétique total et référentiels galiléens.
(La nouvelle origine est mobile, en translation rectiligne uniforme)
La vitesse de translation du point
 est notée
est notée
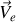 selon la composition des vitesses :
selon la composition des vitesses :
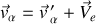 .
.
Le moment cinétique
 et celui des forces extérieures
et celui des forces extérieures
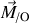 étant reliés par le théorème du moment cinétique :
étant reliés par le théorème du moment cinétique :
 , ils peuvent être modifiés.
, ils peuvent être modifiés.
Dans un référentiel galiléen de sommet
 où les relations entre d'une part les vecteurs position et d'autre part les vecteurs vitesse sont :
où les relations entre d'une part les vecteurs position et d'autre part les vecteurs vitesse sont :
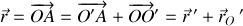
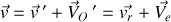
et où les notations de grandeur "relative" et "d'entraînement" ont été adoptées, le moment cinétique s'écrit :
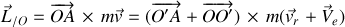
Sa dérivée par rapport au temps prend la forme suivante après simplifications :

où la propriété d'invariance du PFD a été utilisée.
Ainsi et quel que soit le référentiel galiléen de sommet
 , le théorème du moment cinétique est également invariant puisque :
, le théorème du moment cinétique est également invariant puisque :
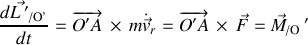 .
.
L'invariance de forme est validée pour le théorème du moment cinétique.
La généralisation à
 particules, appliquée au moment cinétique s'écrit :
particules, appliquée au moment cinétique s'écrit :
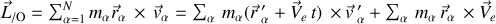
soit :

Si et seulement si le point
 est confondu avec le centre d'inertie
est confondu avec le centre d'inertie
 , le dernier terme s'annule et l'équation permettant le passage d'un moment cinétique à l'autre s'écrit :
, le dernier terme s'annule et l'équation permettant le passage d'un moment cinétique à l'autre s'écrit :
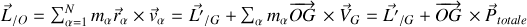
Ces équations permettent donc le transfert du moment cinétique d'un référentiel galiléen à l'autre.
Si
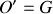 , la modification du théorème du moment cinétique disparaît si
, la modification du théorème du moment cinétique disparaît si
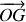 est parallèle à l'impulsion totale.
est parallèle à l'impulsion totale.
Cette propriété et les formules de passage seront utiles dans le cas de système à
 corps dont le corps solide, traité dans le grain 3.
corps dont le corps solide, traité dans le grain 3.




