Syntaxe : Quelques éléments de définition et notations
Pour modéliser une expérience de diffusion, le nombre de particules mises en jeu et la multitude de probables collisions suggèrent l'utilisation d'une méthode statistique.
Une première différenciation est effectuée selon le rôle des particules : cible ou projectile.
La cible, notée ici
(pour impact), est le plus souvent composée de plusieurs particules.
Le paramètre d'impact
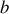des projectiles est rarement complétement contrôlé.
Ainsi les projectiles seront supposés avoir un paramètre d'impact compris entre
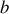et
.
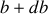Ils seront diffusés entre les angles
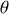et
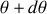. (fig. 21)
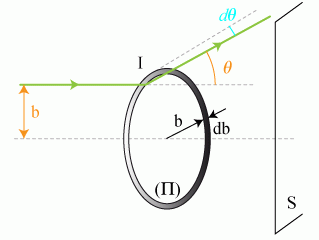
Coté incidence :
Le faisceau incident transporte un nombre
de particules par unité de surface et de temps.
Il couvre une surface
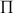de la cible.
Pendant un temps
, le nombre
de particules incidentes vaut :
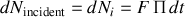
Coté cible :
Si la surface
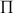de la cible comporte
atomes cibles par unité de volume, répartis sur une épaisseur
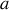, le nombre total de centres diffusants sera égal à :
.
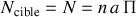La probabilité
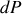pour que les particules incidentes aient un paramètre d'impact compris entre
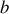et
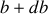correspond au nombre de collisions.
Il vaut :
Coté détection.
La diffusion a eu lieu.
Il faut à présent compter le nombre de projectiles arrivant sur la surface
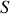d'un détecteur placé sur la surface
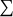des figures 21 et 22.
Une nouvelle notion apparaît, l'angle solide, associée au nombre de projectiles émis par le centre
et captés par le détecteur en
.
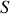Cette notion vient de l'approximation qu'à partir du centre émetteur, les particules qui diffusent selon un angle
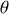traversent
une zone de l'espace délimitée par un cône de sommet
, et d'angle d'ouverture
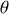, ainsi que des calottes sphériques successives de rayon de plus en plus grand.
Toutes les particules qui traversent la base
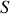du cône sont celles issues de
.
Ainsi toute surface
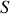de l'espace, susceptible d'être traversée par (ou de recevoir) les particules, peut être caractérisé par un angle "solide" associé à ce cône de base
.
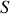Pour évaluer cette nouvelle grandeur, il suffit de remarquer que la base du cône découpe une calotte sphérique
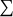dans une sphère de rayon
, correspondant à la longueur de la génératrice du cône et dont le centre est le sommet
du cône.
D'où la définition astucieuse de l'angle solide s'appuyant sur le "volume angulaire" du cône et permettant de s'affranchir de sa longueur.
Définition de l'angle solide :
Noté
, il représente l'angle ‘volumique' du cône qui sous-tend la surface sphérique
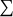de la fig. 22.
Il est défini par le rapport invariant de
l'aire
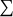de la calotte sphérique découpée par la base du cône (
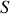) sur la sphère dont le centre est le sommet du cône, divisée par le carré de son rayon.
Soit :
.
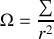L'angle solide
égale la surface découpée dans la sphère de rayon "unité".
Il vaut
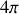si
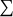représente la sphère complète.
L'intérêt de l'angle solide, outre sa formulation simple, est qu'il peut sous-tendre toute partie de l'espace indépendamment de sa profondeur... par morceaux s'il le faut.
Par conséquent toutes les surfaces quelle que soit leur forme.
De plus, pour les surfaces élémentaires la propriété suivante est vérifiée :
.
Ceci dépend des échelles de calcul et de mesure. (Voir remarque ci-après)
En coordonnées sphériques par exemple, tout élément de surface est décrit par :
.
En plaçant un détecteur dans le plan de
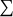perpendiculaire à la direction du faisceau (dans l'axe du faisceau incident),
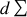définit l'élément de surface élémentaire associé au détecteur.
Ainsi
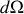devient l'angle solide élémentaire défini autour de l'angle de diffusion
.
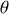Si l'angle
, par symétrie de révolution, varie de
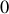à
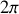, l'angle solide s'écrit :
,
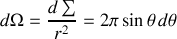Cette relation prédit une détection et une probabilité de détection indépendantes de l'angle
.
Unité d'angle solide:
L'angle solide est sans dimension (rapport de
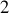surfaces).
Néanmoins il caractérise le produit de
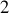angles et son unité est le stéradian (sr).
Méthode : Nombre de particules diffusées
A présent le nombre de particules diffusées pendant
dans l'angle solide
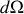peut être calculé.
Il est noté
et associe
1) la probabilité pour que les particules incidentes aient un paramètre d'impact compris entre
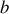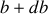et
et 2) la fraction de particules incidentes.
Par définition, le nombre de particules diffusées pendant
dans l'angle solide
:
.
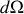Soit, en fonction de
:
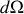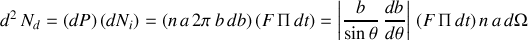
Le nombre de particules diffusées pendant
dans l'angle solide
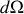dépend :
→ du nombre de particules incidentes sur la cible de surface
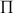pendant
mais aussi
→ de la probabilité de détecter des particules sous l'angle
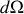.Cette dernière dépend elle même du nombre de centres diffusants.
Ces éléments étant définis, la section efficace, notée
, apparaît via la section efficace différentielle relative
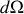selon la définition suivante.
Définition :
La section différentielle efficace relative à
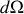est définie par la relation :
Elle représente le nombre de particules diffusées
par unité d'angle solide,
par nombre de centres diffusants (
) et de particules incidentes (
).
Remarque :
Les chocs et collisions atomiques ou moléculaires ont lieu sur des dimensions très faibles comparativement à la surface macroscopique du détecteur.
Ainsi les points de contact individuels
peuvent être confondus avec le point O, centre macroscopique de la cible, sans grand risque d'erreur.
Les figures ont été agrandies par souci de clarté et de lisibilité.
De même les formules ont été volontairement exprimées sous une forme décomposée, exposant les contributions qui participent à la mesure et au calcul.
Remarque : Approximation non explicite.
La source de la diffusion est "centrale" et unique.
Une approximation est sous entendue dans la notion de l'angle solide : pas de collision supplémentaire dans le cône de définition.
En cas de collisions multiples, un comptage de molécules différent est présenté lors du calcul de la pression cinétique.
Cette dernière évalue le nombre de molécules non pas à partir du point "source" mais sur la surface d'arrivée : dans le cas développé, il s'agit des parois d'une enceinte.
Ainsi l'information concernant les propriétés physiques particulières des collisions est perdue mais des contraintes d'homogénéité sont imposées.
