Bien que s'agissant d'un choc, la description dans le modèle de la sphère dure devient une collision (fig. 23).
En effet, un potentiel d'interaction
 peut être défini par :
peut être défini par :


Il s'agit d'un potentiel qui décrit l'interaction d'une particule incidente de paramètre d'impact
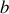 avec une sphère de rayon
avec une sphère de rayon
 impénétrable.
impénétrable.
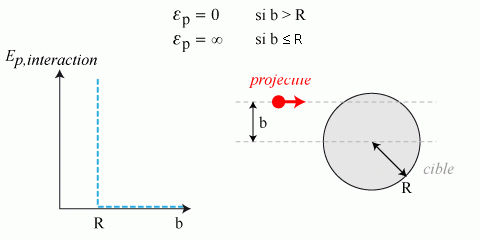
Ainsi si :
 : pas d'interaction.
: pas d'interaction. La particule incidente ignore la cible.
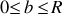 : il y a diffusion de la particule incidente par la sphère
: il y a diffusion de la particule incidente par la sphère : c'est le choc frontal.
: c'est le choc frontal.
La relation entre
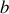 et
et
 correspond à la loi de Descartes sur la réflexion.
correspond à la loi de Descartes sur la réflexion.
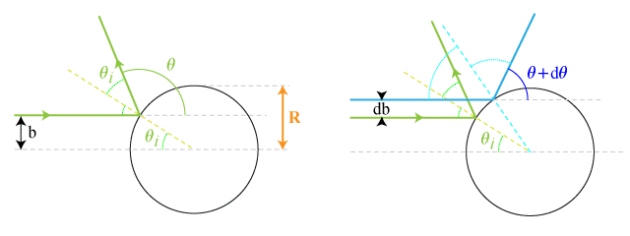
Dans une collision élastique sur une sphère dure immobile, la particule incidente va être « réfléchie » selon la même loi d'angle. (fig. 24)
Entre incidence
 et réflexion
et réflexion
 , les relations suivantes sont obtenues sur la base de considérations géométriques (fig. 24) :
, les relations suivantes sont obtenues sur la base de considérations géométriques (fig. 24) :

La différentielle de cette dernière équation permet de déduire la grandeur suivante :
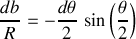
La section efficace différentielle s'écrit :
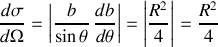
Elle est constante.
La section efficace totale peut être calculée pour l'exemple général suivant :

Cette valeur calculée pour un angle
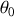 concerne toutes les particules incidentes dans un anneau de paramètres d'impact.
concerne toutes les particules incidentes dans un anneau de paramètres d'impact.
Il est tel que
 à la valeur
à la valeur
 correspondant à l'angle de diffusion
correspondant à l'angle de diffusion
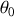 .
.
À noter que la direction de l'angle
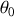 passe par le centre de la sphère.
passe par le centre de la sphère.
Remarque :
Ce calcul ne prend pas en compte la taille des particules incidentes.
Auquel cas, le paramètre d'impact mesurerait la distance entre les CDM.
La valeur de
 vaudrait :
vaudrait :
 , associant ainsi les rayons respectifs des particules incidentes et cibles.
, associant ainsi les rayons respectifs des particules incidentes et cibles.
Attention : Bornes d'intégration et calcul
L'utilisation directe des formules peut conduire à l'intégrale suivante, portant sur le paramètre
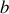 :
:
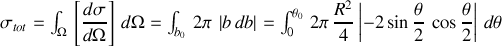
Le calcul direct donne un résultat, un peu moins direct , comparé à la forme précédente.
Le même résultat.




