La modélisation qui suit a constitué un support essentiel à l'expérience.
Ainsi le modèle de diffusion de Rutherford (1911) décrivant une interaction coulombienne entre deux particules chargées a permis de comprendre les résultats expérimentaux de Thomson et de révéler la structure des atomes.
Cette théorie permet de décrire, dans l'espace, les chocs et collisions d'un grand nombre de particules (le flux incident) au moyen
d'une distribution spatiale incluant le nombre de particules traversant une surface donnée et
de la probabilité d'interagir avec des centres diffusants,
et delà, de diffuser dans un secteur de l'espace.
Cette théorie complète et étend les approches et calculs précédents.
Tout comme la partie qui précède, cette théorie peut s'appliquer à des chocs avec contact ou une interaction répulsive.
Suite aux calculs des sections précédentes relatifs à la trajectoire d'une seule particule entrant dans le champ de force d'une particule cible, deux situations peuvent se produire :
soit le projectile est trop éloigné de la cible et il n'y a pas de changement de trajectoire,
soit il s'en approche suffisamment et la « collision ou choc » a lieu.
Pour les besoins de cette description, un nouvel outil d'analyse est construit : la SECTION EFFICACE DE DIFFUSION.
Pour cela, des paramètres sont utiles. Déjà rencontrés dans les précédentes descriptions, ils deviennent ici centraux.
Un premier paramètre important de ce schéma de description : c'est le paramètre d'impact en entrée, noté
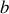(fig. 20).
Le second paramètre prépondérant est l'angle de diffusion en sortie, noté
. Il dépend du premier, pas seulement par la réponse binaire, déviation ou non, mais également parce qu'il caractérise les propriétés de la zone d'impact.
Ces deux paramètres constituent l'ossature du raisonnement permettant le calcul et la mesure de la déviation.
Jusqu'à présent, les descriptions impliquaient uniquement deux particules.
Ces études serviront de base pour une généralisation.
Dans le cas d'un flux de particules envoyé sur plusieurs cibles, et de manière générale, l'angle de diffusion va dépendre du paramètre d'impact de chaque projectile par rapport aux cibles, supposées fixes.
La fig. 20 décrit le cas de la diffusion de Rutherford avec les notations ci-dessus.
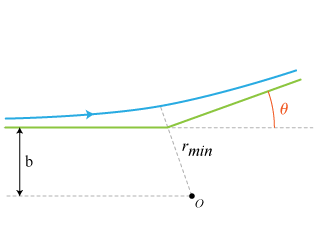
Les valeurs possibles de l'angle de diffusion dépendent également du type d'interaction, de ses paramètres physiques et donc du potentiel d'interaction associé par exemple au champ coulombien ou gravitationnel.
L'objectif consistera à obtenir une expression analytique de l'angle de diffusion en fonction des paramètres physiques représentatifs de ce(s) potentiel(s).
Dans le cadre de ce cours, la notion de section efficace de diffusion sera appliquée au modèle du potentiel de la sphère dure.
