Syntaxe : Des variables, des fonctions.
En mécanique et pour un système évoluant dans l'espace au cours du temps
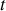, cette théorie utilise les éléments suivants.
Pour décrire le système physique, un ensemble de variables est construit autour de
un ensemble de coordonnées généralisées propres au système, notées
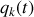où
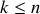est un entier inférieur au nombre de variables nécessaires à la description.À ces coordonnées sont associées
les vitesses généralisées
, dérivées par rapport au temps des coordonnées précédentes.
Ces couples constituent
variables et la base du formalisme lagrangien.
La description du système physique est alors contenue dans une fonctionnelle
reliant ces variables généralisées.
Si, en mécanique, l'évolution du système physique est décrit par sa position dans l'espace et des coordonnées ou variables de position, hors mécanique, la coordonnée généralisée représente toute variable décrivant le système.
En thermodynamique, la complexité est telle que l'étude porte sur des successions d'états d'équilibre décrits par les coordonnées généralisées que sont la température, le volume, la pression, etc...
Le temps ne joue pas le même rôle dans ces deux domaines.
Fondamental : Le résumé en mécanique.
Une fonctionnelle particulière, notée
, est fonction des énergies cinétique
et potentielle
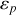selon la relation générale :
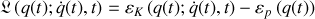
Elle dépend des variables du problème : les coordonnées généralisées
, leurs vitesses généralisées
, ainsi que du temps
.
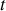Une fonctionnelle, dénommée "action", est construite sur l'intégrale indéfinie suivante, effectuée au cours du temps et pour une trajectoire possible dans l'espace
selon :
La minimisation de cette action entre deux instants précis
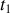et
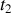, évaluée sur des trajectoires différentes mais qui se rejoignent exactement aux deux instants extrêmes, permet de définir une trajectoire particulière minimisant la fonctionnelle action ci-dessus.
Cette trajectoire, objet de la recherche, est régie par les
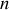équations suivantes :
Ce sont les équations du mouvement d'Euler-Lagrange du système étudié.
Remarque : Quelques précisions et définitions
Si
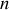coordonnées sont utiles à la description du système, les équations d'Euler Lagrange constitueront un système de
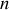équations différentielles du second ordre couplées.
L'entier
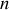est le nombre de degrés de liberté (DL) nécessaires à la description du mouvement.
Et la formulation présentée ci dessus caractérise le formalisme de Lagrange du second type.
En mécanique, les variables généralisées
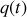représentent toute variable servant à décrire le mouvement du système étudié (distance ou angle) ; cependant si une relation associe les coordonnées entre elles, elle constitue une contrainte au mouvement. Cette relation devrait permettre de réduire d'une unité le nombre d'inconnues sinon le nombre de variables utilisé pour la description est supérieur d'une unité au nombre de degrés de liberté.
Les contraintes sont explicitement prises en compte dans :
le formalisme du premier type qui sera brièvement abordé dans la seconde remarque qui suit l'explication ci après,
et le chapitre des multiplicateurs de Lagrange.
Mécanique lagrangienne et mécanique vectorielle.
Par analogie avec le second postulat de Newton,
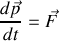, chaque équation peut être perçue comme l'évolution au cours du temps d'une impulsion généralisée (terme de gauche) produite par un ensemble de forces généralisées (terme de droite). Mais sous une forme scalaire.
L'application aux coordonnées cartésiennes ci après fournit des éléments explicatifs.
Explication : Particule dans un espace cartésien.
En coordonnées cartésiennes
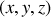et pour une particule élémentaire soumise à une force conservative (dérivant d'une énergie potentielle ne dépendant que de sa position, soit
), les trois équations différentielles dérivées du formalisme lagrangien sont identiques à celles du PFD (Principe Fondamental de la Dynamique ou second principe de Newton) exprimées selon chacune des directions
,
ou
.
Le membre de gauche compose la partie inertielle (masse * accélération) et celui de droite, celles des forces appliquées, dérivant d'une énergie potentielle, selon chaque axe de coordonnée.
Cette exemple permet
d'introduire la notion d'accélération généralisée et inertielle, à gauche, et de force généralisée à droite, mais également et de façon similaire à la mécanique vectorielle,
de tenir compte des forces susceptibles de s'ajouter à droite, comme les forces de frottement, et de mesurer leurs effets selon les directions considérées.
Remarque : Contraintes, forces de contrainte et PFD modifié.
Quand des contraintes existent (mouvement sur un cercle par exemple, ou toute relation vérifiée par les variables généralisées) et notées
, le formalisme de Lagrange du premier type consiste à introduire le gradient des équations de contraintes dans le second postulat de Newton sous forme de forces de contraintes.
Ces forces de contrainte sont ainsi déduites des contraintes matérielles subies par le système.
Par définition, une contrainte réduit la généralité du mouvement.
Par exemple un mouvement plan, un fil inextensible de longueur
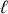en mouvement dans l'espace... produisent respectivement les relations :
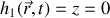, et
) dont le gradient sera proportionnel à la force de contrainte.
Une contrainte dans l'espace à
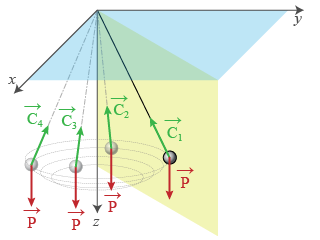
dimensions confine le mouvement sur une surface : ci-dessus, mouvement plan ou sphérique (voir Fig. 1 pour des positions quelconques du pendule).
De même pour contraindre le mouvement d'une particule selon la contrainte
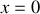, donc avoir un mouvement dans le plan
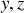, la force de contrainte doit s'exercer perpendiculairement à ce plan pour y plaquer la particule.
Le PFD modifié s'écrit :
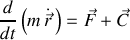
où la résultante des forces à l'origine du mouvement
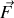, souvent issue d'une énergie potentielle, est distinguée de la force de liaison
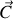, issue quant à elle de la contrainte selon la relation :
Sous ce nouvel éclairage, l'énergie potentielle apparaît comme une contrainte particulière : de fait le mouvement le moins contraint est le mouvement libre.
Le coefficient de proportionnalité
est un multiplicateur de Lagrange.
Il est porteur de la dimension de la force. (voir le chapitre VI sur les "multiplicateurs de Lagrange")
Et il est à l'origine de la dénomination de "formalisme lagrangien du 1er type".
Géométriquement,
les forces à l'origine du mouvement,
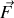, sont dans le plan de ce dernier,
la force de contrainte va en plus s'exercer perpendiculairement à la trajectoire.
Par exemple, seule une force de liaison selon l'axe vertical peut maintenir un mouvement dans un plan horizontal.
Cette propriété est portée par le gradient de la contrainte.
Cette remarque illustre à quel point forces et vecteurs ne sont jamais loin... en mécanique.
La généralisation à plusieurs contraintes est une addition de cette même procédure.
