En résumé et sur le plan pratique, la mise en œuvre de la théorie lagrangienne nécessite la maîtrise de deux étapes:

• Écrire les énergies : cinétique 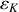 et potentielle  .

  • En déduire le lagrangien

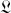
• Dériver autant d’équations que de coordonnées généralisées (degrés de liberté).

  • Les résoudre, si possible.

Un savoir-faire est exigé pour réaliser chaque étape :

• Identifier, délimiter le système mécanique à étudier (nombre de points matériels, solides).

  Déterminer ses symétries et contraintes : mouvement plan, sphérique, rotations... → Différencier les coordonnées, donc les variables (coordonnée, vitesse) utiles pour décrire le mouvement.

  Ce point prend tout son sens dans l'étude de systèmes mécaniques complexes.

• Calculer la grandeur scalaire et additive 'énergie cinétique' 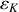de tout le système

  → Exprimer les vecteurs vitesse et leurs modules au carré.

• Identifier la ou les énergies potentielles mises en jeu , grandeurs également additives, en identifiant les forces à l'origine du mouvement.

  → Gérer  l'opérateur gradient qui associe à une force son énergie potentielle.

• Effectuer la différentiation d'une fonction de plusieurs variables, une fonction de fonctions ou fonctionnelle, et surtout maîtriser les nuances entre dérivations d'une variable implicite (nécessitant une dérivée totale) ou explicite (pouvant supporter une dérivée partielle)