Dans ce paragraphe, seule la translation (mouvement rectiligne) est considérée.
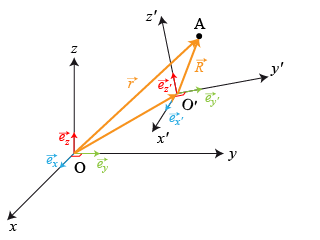
La figure (Fig. 12) représente un cas général.
Pour caractériser le cas de figure développé dans ce paragraphe, il faudrait que les axes du repère mobile soient parallèles à ceux du repère fixe puisque seule sa translation est prise en compte.
La position du point matériel dans le repère mobile est décrite par
.
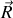Lorsque le référentiel mobile est en translation par rapport au référentiel 'fixe', la composition des vitesses permet d'écrire :
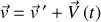où les notations sont toujours différenciées entre repérages dans le référentiel fixe ou mobile.
La vitesse
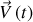est celle du point
soit
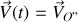
Le lagrangien de la particule s'écrit toujours :
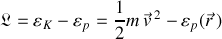
La composition des vitesses peut être reportée dans le lagrangien pour produire l'expression :
Ce lagrangien est également celui du référentiel mobile.
Les équations du mouvement de Lagrange qui vont être dérivées doivent porter sur les variables dans le référentiel mobile soit
.
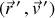Toutes les dérivées portant sur l'énergie potentielle contribueront à la partie 'référentiel fixe' et inchangée des équations du mouvement.
Les deux termes additifs de l'énergie cinétique dans le référentiel mobile contiennent la vitesse de translation du référentiel mobile, une fonction du temps.
Des deux termes, seul celui en produit scalaire avec
va donner une contribution intéressante.
Le second est fonction uniquement du temps.
Il peut être considéré comme constant dans le lagrangien, par rapport aux variables 'mobiles'.
Le terme en produit scalaire peut être réécrit sous la forme :
ou finalement :
L'accélération
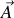du référentiel mobile apparaît ainsi qu'un terme supplémentaire du type
qui peut être ignoré.
Fondamental : Lagrangien dans un référentiel accéléré
Le lagrangien exprimé dans le référentiel mobile en translation accélérée est modifié selon :
Apparaît un terme additif, porteur de l'accélération subie, sous la forme d'une énergie potentielle particulière.
Les équations du mouvement d'Euler Lagrange correspondantes :
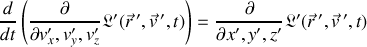
En écriture vectorielle :
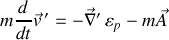
Un champ de force homogène additif apparaît, associé à l'accélération d'entraînement du référentiel mobile et à sa force d'inertie.
Exemple : Bille sur un plan incliné mobile
En application directe , une reprise de l'exercice 4 du chapitre I-B de ce cours est proposée.
L'approximation du point matériel est assumée dans ce qui suit.
Néanmoins l'effet de la rotation de la bille peut être pris en compte dans un second temps sachant qu'en cas de roulement sans glissement, seule l'énergie cinétique est modifiée.
L'objet se déplaçant sur le plan incliné, non fixé, sous l'effet de la pesanteur est décrit par les énergies cinétique et potentielle suivantes :
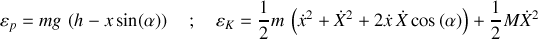
Pour construire le lagrangien
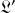de la bille dans le référentiel mobile, rien que la bille, ce lagrangien total doit être sous la forme suivante :
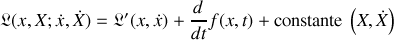
La variable généralisée décrivant le mouvement dans le référentiel mobile est
.
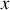Le lagrangien total s'écrit :
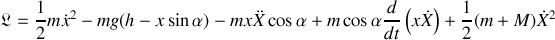
où les deux derniers termes peuvent être ignorés.
Le lagrangien dans le référentiel mobile s'écrit :
L'accélération d'entraînement apparaît dans le terme contribuant à la force généralisée.
L'équation du mouvement de la bille du chapitre 1-B est obtenue en écrivant l'équation d'Euler-Lagrange pour x.
Mais cette équation, seule, est incomplète pour la résolution du mouvement de la bille.
Il faut donc également décrire le mouvement du plan incliné, rien que le plan incliné.
Le mouvement du plan incliné dépend de celui de l'objet, le système étant couplé.
Pour cela il faudra se placer dans le référentiel de la bille et ignorer son mouvement : ses variables
sont donc constantes.
Pour avoir cette forme de lagrangien,
le lagrangien mobile du plan s'écrit :
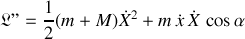
Deux termes ont également été ignorés.
La variable
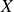est une coordonnée cyclique, exprimant une conservation de quantité de mouvement.
L'équation d'Euler-Lagrange pour la variable X, dérivée de
, permet de retrouver le mouvement du plan incliné seul qui trouve son origine dans celui de la bille.
Attention : Mise au point
Comme souvent dans ce cours, le traitement de cet exercice n'est pas la résolution du problème au sens scolaire du terme.
Il s'agit juste d'analyser les articulations entre une vision complète et bien posée d'un problème (ce qui suppose sa maîtrise totale et de prime abord) avec celle parcellaire d'une analyse nouvelle, progressive où chaque élément manquant apparaît sous une forme plus ou moins directe.
Il s'agit là d'une forme d'apprentissage par le questionnement, par la recherche.
C'est la raison pour laquelle les mêmes exercices sont repris.
