Dans un référentiel non galiléen comme analysé précédemment, la variation d'impulsion au cours du temps vaut :
où apparaissent résultante des forces et forces d’inertie (ou pseudo forces).
Le passage au formalisme lagrangien s'effectue par un retour aux équations sources, celles mettant en jeu l'énergie cinétique totale et toutes les forces généralisées, réelles et d'inertie, s'appliquant sur le système de particules selon :
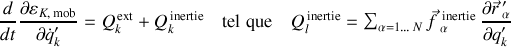
Quand ils existent, les termes en
apparaissent dans le second membre de l'équation sous forme de forces généralisées d'inertie... comme explicité plus haut dans l'analyse des contributions de chaque terme.
Deux cas sont considérés à titre d'exemples.
L'additivité des éléments constitutifs du lagrangien s'accompagnant d'une composition des mouvements permet de déduire les mouvements plus complexes.
Exemple d'un référentiel accéléré par rapport à un référentiel galiléen
Une application directe de l'expression de la force généralisée ci-dessus pour une accélération
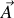identique pour toutes les particules, produit la force généralisée suivante :
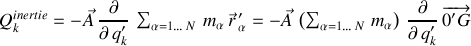
La sommation sur toutes les particules présentes met en évidence, à la masse totale près, la position du centre de masse
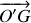dans le référentiel non galiléen.
Référentiel en rotation par rapport à un référentiel galiléen
L'expression du lagrangien, développée précédemment, est écrite sous la forme
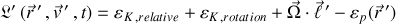
Les contributions inertielles sont contenues dans l'énergie cinétique de rotation et un potentiel inertiel
contenant le moment cinétique précisé ci-après :
Ces rappels permettent notamment d'identifier les dépendances en variables
Le lagrangien permet de déduire aisément les forces d'inertie généralisées suivantes :
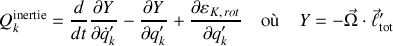
La définition de
a été choisie pour permettre une écriture mnémotechnique.
L'expression des forces généralisées est compréhensible au vu des dépendances en
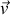et
du moment cinétique total ainsi que de l'énergie cinétique de rotation (en
).
