Ce cas, le plus complet et complexe, n'est que la superposition des deux situations précédentes.
La composition des vitesses s'écrit :
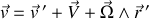
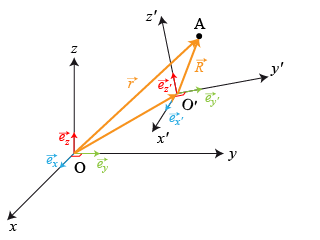
Le lagrangien tenant compte de tous les mouvements de référentiels (translation+rotation) s'écrit :

La différentielle de ce lagrangien en fonction des variables du problème vaut


Apparaissent directement l'impulsion généralisée ainsi que toutes les contributions des dérivées partielles du lagrangien.
Pour le point matériel, les équations du mouvement en référentiel non galiléen du formalisme lagrangien sont en adéquation avec celles de Newton.
Démonstration :
La différentielle de l'énergie cinétique de rotation suivante :

utilise le produit scalaire suivant :

perçu plus loin comme un produit mixte et dont la différentielle est
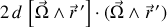
où
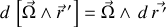
Il ne reste plus qu'à effectuer une permutation circulaire dans le produit mixte résultant pour déduire :

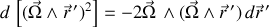
Ce calcul constitue un excellent exercice pour contrôler ses acquis mathématiques sur les différentielles et les opérations vectorielles.




