Le mouvement dans le référentiel "fixe"
est régi par une composition des vitesses donnée par :
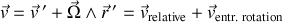
Les "primes" étant réservés au référentiel mobile
, l'entraînement apparaît dans le terme de vitesse angulaire (de rotation).
Dans ce cas de figure, le point
de la Fig. 12 est confondu avec
.
Seules subsistent les rotations du référentiel mobile, portées par
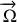, et subies par ses axes.
Le lagrangien complet s'écrit :
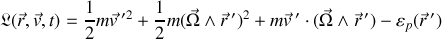
où tous les termes sont à conserver dont les deux contributions énergétiques de la rotation.
Ainsi :
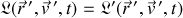
En présence de la rotation, tous les éléments sont naturellement exprimés dans le référentiel mobile.
Ce lagrangien peut également s'écrire selon les notations :
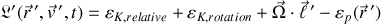
La permutation dans le produit mixte met en évidence le moment cinétique de la particule.
Les trois équations d'Euler-Lagrange du mouvement composent l'équation vectorielle suivante :
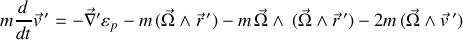
Une étape intermédiaire est représentée par l’impulsion généralisée ou quantité de mouvement :
dont les dérivées par rapport au temps sont explicites et contribuent aux équations du mouvement ci-dessus.
Remarque : L'hamiltonien dans un référentiel en rotation
Le calcul de l’hamiltonien « relatif » défini par :
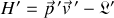s’écrit, tous calculs effectués :
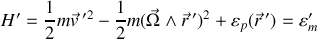
Apparaît une forme d'énergie cinétique de rotation « centrifuge » (avec un signe moins) mais nulle énergie liée à la force d'inertie de Coriolis !
Cette dernière est, par construction, vectoriellement perpendiculaire à la vitesse.
Le produit scalaire annule toute forme de travail de cette pseudo-force et par conséquent, d'énergie susceptible d'être comptabilisée dans l'énergie mécanique totale qu'est l'hamiltonien.
Il est utile néanmoins de préciser que, le système étant conservatif (puisque soumis à une énergie potentielle), l'énergie mécanique qui est conservée est celle dans le référentiel fixe et non pas celle du référentiel en rotation.
Remarque : Technique
Dans les calculs, beaucoup d'indications ont été "semées".
Néanmoins certains calculs ont été volontairement laissés pour permettre des pratiques personnelles sur les opérations vectorielles de dérivation.
