L'onde incidente est divergente et est donc constituée d'une infinité de rayons contenus dans le cône d'émission de la source. Un rayon particulier issu de la source (cf. Fig.20) se réfléchit en partie au point
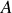 sur le haut de la lame. De façon complémentaire une fraction du rayon incident est transmise à travers la lame en subissant une réfraction avant de se réfléchir au point
sur le haut de la lame. De façon complémentaire une fraction du rayon incident est transmise à travers la lame en subissant une réfraction avant de se réfléchir au point
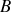 du bas de la lame pour ressortir au point
du bas de la lame pour ressortir au point
 après une seconde réfraction. Au point
après une seconde réfraction. Au point
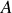 , l'onde incidente d'amplitude
, l'onde incidente d'amplitude
 subit donc une division d'amplitude puisque le champ réfléchi s'écrit
subit donc une division d'amplitude puisque le champ réfléchi s'écrit
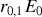 et le champ transmis
et le champ transmis
 . Les coefficients
. Les coefficients
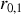 et
et
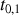 sont respectivement les coefficients de Fresnel de réflexion et de transmission en amplitude du dioptre air-lame. Ces coefficients sont définis par les relations de Fresnel qui traduisent la continuité du champ électrique et de sa dérivée à l'interface. En incidence normale, on peut montrer que
sont respectivement les coefficients de Fresnel de réflexion et de transmission en amplitude du dioptre air-lame. Ces coefficients sont définis par les relations de Fresnel qui traduisent la continuité du champ électrique et de sa dérivée à l'interface. En incidence normale, on peut montrer que

avec la relation constitutive de Fresnel

Pour le dioptre air-verre,
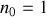 et
et
 . Le coefficient de réflexion
. Le coefficient de réflexion
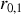 est alors négatif et vaut sensiblement 20% ce qui conduit à une transmission de 80% du champ incident dans la lame. Le caractère négatif du coefficient de réflexion traduit le fait que l'onde est réfléchie en opposition de phase avec le champ incident ce qui peut aussi se voir en écrivant
est alors négatif et vaut sensiblement 20% ce qui conduit à une transmission de 80% du champ incident dans la lame. Le caractère négatif du coefficient de réflexion traduit le fait que l'onde est réfléchie en opposition de phase avec le champ incident ce qui peut aussi se voir en écrivant
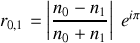
Une réflexion sur le dioptre air-verre se fait donc avec un changement de phase de
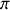
Si le dioptre du bas (noté 2) est le dioptre milieu-air, nous pouvons réutiliser ces relations en interchangeant les indices et l'on obtient

Il n'y a pas de changement de phase dans ce cas et l'on voit que
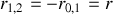 et
et
 .
.
Remarque :
On peut facilement s'étonner de voir un coefficient de transmission de
 . Il faut pour comprendre que cette valeur n'est pas ridicule se rappeler que c'est l'énergie qui se conserve ce qui impose
. Il faut pour comprendre que cette valeur n'est pas ridicule se rappeler que c'est l'énergie qui se conserve ce qui impose
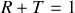 en absence d'absorption (milieux diélectriques).
en absence d'absorption (milieux diélectriques).
L'énergie est obtenue en écrivant le module du vecteur de Poynting
 . Il est facile de vérifier que
. Il est facile de vérifier que
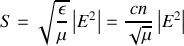 . D'autre part le coefficient de réflexion en intensité (en incidence normale) est donné par
. D'autre part le coefficient de réflexion en intensité (en incidence normale) est donné par
 et le coefficient de transmission en intensité par
et le coefficient de transmission en intensité par
 .
.
Pour des milieux non magnétiques on voit que la condition
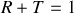 appliquée à l'interface
appliquée à l'interface
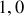 conduit à
conduit à
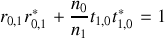
Il est à première vue surprenant que l'amplitude transmise puisse être supérieure à celle de l'onde incidente mais il n'y a pas de contradiction car ce qui importe c'est la conservation de l'énergie. Il est facile de vérifier que les modules au carré,
 et
et
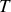 , des coefficients de réflexion et de transmission vérifient
, des coefficients de réflexion et de transmission vérifient
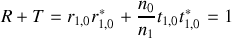
Nous voyons donc que le champ incident se divise en amplitude à chaque fois qu'il rencontre un dioptre. Les rayons issus de cette division ont une amplitude qui dépend du nombre de divisions effectuées. Ainsi le rayon incident d'amplitude
 se divise en deux rayons d'amplitude
se divise en deux rayons d'amplitude
 et
et
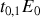 ce qui conduit à un rayon émergeant en
ce qui conduit à un rayon émergeant en
 d'amplitude
d'amplitude
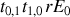 . Nous pouvons facilement extrapoler le résultat aux rayons qui subissent des réflexions multiples pour trouver que leurs amplitudes seraient
. Nous pouvons facilement extrapoler le résultat aux rayons qui subissent des réflexions multiples pour trouver que leurs amplitudes seraient
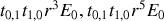 ....Les rayons émergeants ont donc une amplitude qui varie comme
....Les rayons émergeants ont donc une amplitude qui varie comme
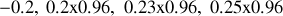 . Il s'ensuit que les deux premiers rayons ont des amplitudes équivalentes alors que les rayons suivants ont des amplitudes négligeables. Il est clair que les interférences observées sur l'écran proviennent de la superposition des deux premiers rayons que l'on appellera
. Il s'ensuit que les deux premiers rayons ont des amplitudes équivalentes alors que les rayons suivants ont des amplitudes négligeables. Il est clair que les interférences observées sur l'écran proviennent de la superposition des deux premiers rayons que l'on appellera
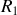 et
et
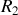 . Ces deux rayons sont issus du même rayon incident dont l'amplitude est divisée en
. Ces deux rayons sont issus du même rayon incident dont l'amplitude est divisée en
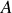 . Ils présentent donc à leur sortie de la lame une cohérence parfaite et ils interfèrent car ils ne parcourent pas le même trajet dans la lame. La connaissance de la différence de marche entre ces deux rayons permet de prédire le rayon des anneaux.
. Ils présentent donc à leur sortie de la lame une cohérence parfaite et ils interfèrent car ils ne parcourent pas le même trajet dans la lame. La connaissance de la différence de marche entre ces deux rayons permet de prédire le rayon des anneaux.
Remarque :
Ce phénomène est visible quel que soit le rayon considéré (un rayon qui se divise est forcément cohérent spatialement avec lui même) ce qui permet de comprendre pourquoi une source étendue a priori incohérente spatialement permet l'observation des anneaux.




