Nous considérons la réflection d'une lumière monochromatique sur une lame mince d'épaisseur
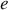et d'indice
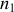éclairée en incidence normale. Nous avons vu que la différence de marche entre le rayon réfléchi sur le dioptre supérieur et celui réfléchi sur le dioptre inférieur est
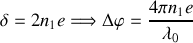
La couche mince possède une réflectivité
qui dépend des indices des différents milieux et de l'épaisseur
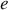de la lame. Le champ total réfléchi est donné par
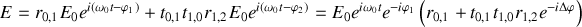
avec
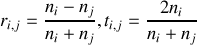
Le champ peut s'écrire également
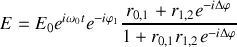
Le dénominateur contient la contribution des ondes multiples et peut être approximé à 1 si
. Il s'ensuit que le champ réfléchi s'écrit :
Le système est antireflet si, par interférence destructive par réflexion, le champ réfléchi est nul ce qui impose
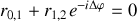
On peut facilement se convaincre (voir Figure 24) en utilisant une représentation de Fresnel que la seule solution est
.
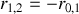Représentation de Fresnel illustrant la somme de deux ondes d'amplitude
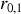et
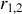déphasées de
Si les coefficients de Fresnel
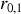et
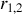sont de même signe, il faut que la différence de phase entre les ondes se réfléchissant sur les deux interfaces vérifie
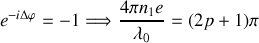
L'épaisseur de la lame antireflet doit donc vérifier
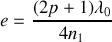(5)
De plus l'indice de la lame mince doit satisfaire l'égalité des coefficients de réflexion soit
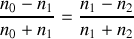
Pour une lame antireflet placée dans l'air cette condition conduit à
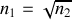
Comme les indices en optique sont supérieurs à 1, l'équation (6) ne peut être satisfaite que si l'on dépose sur le milieu 2 une couche d'indice
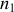inférieur à
. L'épaisseur la plus petite qui correspondra à un coefficient de réflexion nul sera
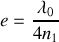
Il s'agit d'une lame quart d'onde pour la longueur d'onde
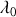. Il est clair que la condition d'anti-reflet n'est valide que pour cette longueur d'onde
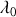et que dès que l'on s'écarte de cette radiation la réflexion sur la lame devient de nouveau possible comme le montre la figure 24.
Comme seule la longueur d'onde de centrage n'est pas réfléchie, les lames traitées anti-reflet préstenent une couleur caractéristique bleu-violet ou rouge car pour ces longueurs d'onde le coefficient de réflexion n'est pas nul.
Attention :
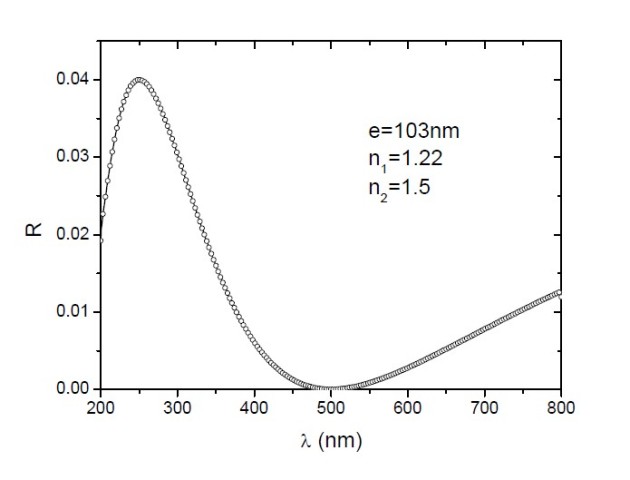
Nous retiendrons donc qu'une couche antireflet déposée sur une milieu d'indice
sera anti-reflet pour la radiation
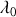si
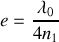avec
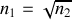
Ainsi une lame antireflet déposée sur du verre d'indice
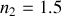doit avoir un indice de
et une épaisseur donnée par l'équation (5). L'inconvénient majeur de ce type de revêtement est qu'il faut pouvoir trouver un matériau d'indice 1.22 ce qui est quasi impossible à trouver en pratique comme le montre le tableau ci-dessous
Remarque :
Les lames minces antireflet sont actuellement fabriquées en utilisant plusieurs couche voire même des empilements multicouche. La méthode la plus simple consiste à empiler une couche de haut indice suivie par une couche de bas indice comme par exemple
suivi de
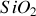. Les coefficients de reflexion deviennent :
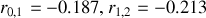et
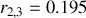
et le champ est réfléchi est donné par
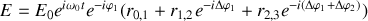
Il est facile de trouver les épaisseurs des couches 1 et 2 en utilisant la construction de Fresnel dans laquelle le centre des cercles de rayons
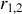et
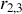sont aux deux extrémités du vecteur de Fresnel
.
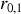Remarque :
Il existe deux solutions correspondant aux deux points d'intersection des deux cercles. La position de ces points définit la valeur des phases
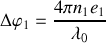et
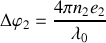et par conséquent celles des épaisseurs des deux couches. Pour l'empilement verre,
,
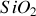et la longueur d'onde de centrage
il y a antireflet si
et
.
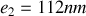Complément :
La fabrication de filtre interférentiel à bande très étroite est basée sur le principe d'empilement de couches minces diélectriques. Il est alors possible de fabriquer un matériau qui ne réfléchit pas du tout une longueur d'onde précise tout en la transmettant intégralement.
