Le rayon des anneaux dépend évidemment de leur ordre. A l'ordre
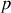, on a donc
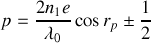
Le calcul précédent montre que l'ordre d'interférence décroît quand
augmente. L'ordre d'interférence est donc plus élevé au centre de la figure. Si nous appelons
cet ordre, il vérifie
Il est clair que cet ordre n'est pas forcément entier ce qui montre que le centre de la figure n'est pas nécessairement brillant.
Exemple :
Si l'on a une lame de verre d'indice
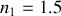, d'épaisseur
et éclairée à
on a :
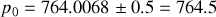ou
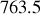
Soit
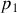l'ordre d'interférence qui correspond au premier anneau brillant on a alors
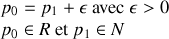
Dans notre exemple on voit que cela conduit à
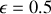et
ou
. Dans ce cas comme l'ordre au centre est de type demi-entier le centre de la figure sera noir.
Soit
le numéro d'un anneau brillant (
est le premier anneau,
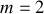le second etc..). Nous voyons que l'ordre
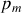de cet anneau diffère du numéro de l'anneau (il est facile de vérifier que
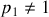). Toutefois, il est possible d'écrire que
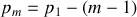
A l'ordre
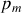qui correspond à l'anneau brillant
on a donc
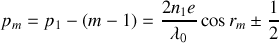
ce qui conduit à
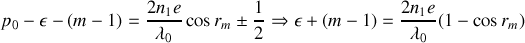
Nous voyons en particulier que la différence de phase qui correspond à l'anneau brillant numéro
est donnée par
Si l'on fait l'hypothèse que le rayon angulaire des anneaux est petit alors
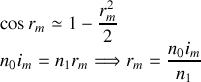
Il s'ensuit que le rayon angulaire
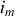de réflexion de l'anneau brillant numéro
est donné par
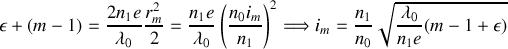
Le rayon angulaire d'un anneau sombre suit évidemment la même loi, mais il diffère de celui de l'anneau brillant d'une valeur 1/2 qui peut être incluse dans l'ordre fractionnaire
. Du point de vue expérimental, il convient de remarquer que la mesure effectuée est toujours celle du rayon de l'anneau et non celle du rayon angulaire. Pour cela on utilise une lentille de grande focale
ou un viseur réglé par autocollimation sur l'infini. Comme le rayon angulaire des anneaux est faible nous pouvons assimiler l'angle de réflexion à sa tangente et comme l'indique la figure il est facile de voir que
Rappel :
Comme il s'agit d'interférences à deux ondes l'intensité mesurée en un point
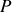de l'écran vérifie
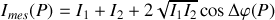
soit pour des ondes de même intensité
ce qui s'exprime en fonction du rayon
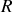des anneaux par
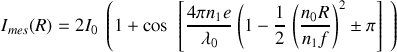
soit
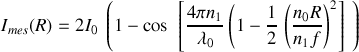
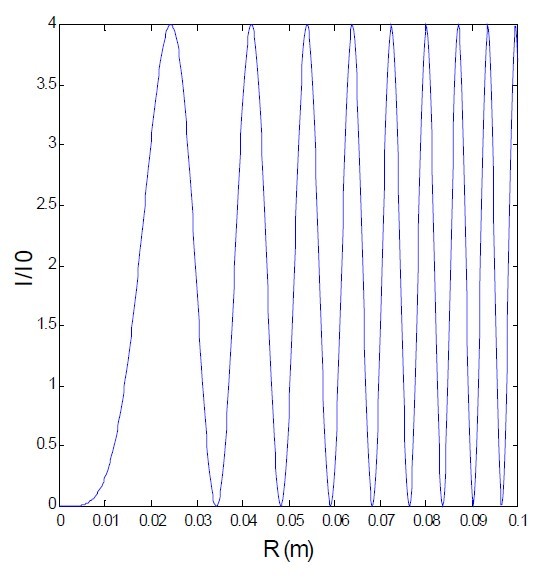
La figure 22 représente l'intensité normalisée des anneaux d'interférences observés pour une lame mince d'indice
et d'épaisseur
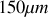éclairée par une lampe à vapeur de sodium en fonction de la distance au centre de l'écran.
Remarque :
Condition de planéïté de la lame :
Pour observer correctement les anneaux il faut que les deux faces de la lame soient bien planes. Tout écart à la planéïté a pour effet de distordre les anneaux. On peut admettre que les anneaux restent bien visibles si l'ordre d'interférence
ne change pas de plus d'une valeur demi-entière.
Dans le visible cet écart ne doit donc pas excéder
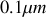ce qui correspond au poli optique.
