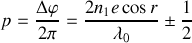Les rayon
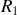et
sont parallèles entre eux après les diverses réflexions. Pour connaître leur différence de marche il convient d'établir la différence de chemin optique parcourue par les deux ondes à l'issue de leur division en
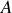(cf. Fig.20).
Remarque :
A partir des points
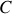et
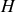les deux rayons parcourent les mêmes chemins optiques. La différence de marche est donc
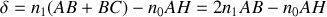
soit
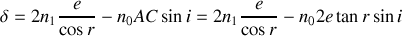
En utilisant la loi de Snell-Descartes,
, nous obtenons
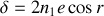
Cette différence de marche correspond à une différence de phase entre le rayon 2 et le rayon 1 qui est égale à
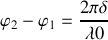
Il convient de se souvenir alors que le rayon
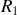a subi un déphasage de
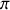à la réflexion ce qui n'est pas le cas du rayon
. Il s'ensuit que
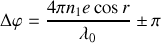
Nous voyons ainsi que la différence de phase entre les deux rayons
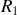et
est obtenue en faisant la somme des différences de phase dues à la propagation et à la réflexion soit
avec
et
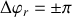
La différence de marche est donc donnée par
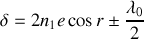
Une façon plus claire de mettre en évidence cette différence de phase est de revenir aux amplitudes des deux rayons. Au point
d'observation sur l'écran se superposent deux rayons dont on peut représenter le champ par
avec
.
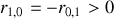On voit tout de suite que c'est le changement de signe du coefficient de réflexion sur le premier dioptre qui impose le changement additionnel de phase de
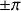. Nous retiendrons le résultat important suivant :
Attention :
Lors de la division d'amplitude, des réflexions de nature différente comme la réflexion sur le dioptre air-verre et celle sur le dioptre verre-air entraînent un changement additionnel de phase de
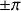à la réflexion. Ce changement de phase est appelé changement de phase à la réflexion.
Remarque :
Le déphasage entre les deux rayons ne dépend que :
de l'épaisseur de la lame et de son indice
de l'angle de réfraction dans la lame donc de l'angle d'incidence par application de la loi de Snell-Descartes
de la longueur d'onde d'observation
Il en résulte que le déphasage est constant pour une lame et une longueur d'onde données si l'angle d'incidence (égal à l'angle de réflexion) est constant soit
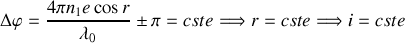
Le lieu des points d'incidence constante à partir de la source est un cône de demiangle au sommet
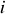. On voit donc de suite qu'un déphasage constant correspondra à des rayons incidents donc réfléchis ayant tous la même inclinaison ce qui explique pourquoi
on observe des anneaux si l'on place l'axe principal de la lentille perpendiculairement à la lame
les anneaux sont qualifiés de franges d'égale inclinaison.
les franges sont localisées à l'infini et que les anneaux sont observables dans le plan focal image d'une lentille mince
Nous notons que les anneaux brillants correspondent à un déphasage multiple de
ce qui donne leur ordre d'interférence
avec
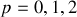
L'ordre d'interférence est demi-entier pour les anneaux sombres.
D'une façon générale pour un angle
on peut calculer un ordre
quelconque (fractionnaire) qui vérifie
