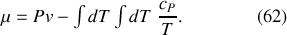L'enthalpie libre d'un système composite, constitué de plusieurs espèces chimiques ou de plusieurs phases d'un ou plusieurs constituants, peut être considérée comme la somme des enthalpies libres des différents constituants :
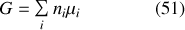
Dans ce cas, le travail chimique s'écrit sous la forme :
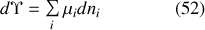
En différenciant la relation (51) et en tenant compte de la quatrième des équations (48), on obtient la première « relation de Gibbs-Duhem »
, généralisation de l'égalite différentielle (47) :
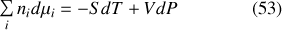
Il est remarquable que cette relation de Gibbs-Duhem établisse un lien différentiel entre les potentiels chimiques à pression et températures constantes. Par exemple pour un mélange binaire, la connaissance d'un des potentiels chimiques conduit à la connaissance de l'autre par simple intégration de l'équation :
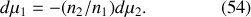
Une autre relation s'obtient à partir de la différentielle de l'entropie généralisée. En effet, d'après l'équation (45) généralisée à plusieurs constituants :
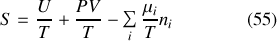
Or, la généralisation à plusieurs constituants de la relation thermodynamique fondamentale donnée par la première des équations (48) permet d'écrire :
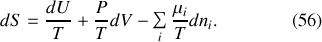
La différenciation de l'équation (55) conduit donc à la seconde relation de Gibbs-Duhem :
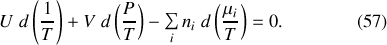
Remarque :
Les deux relations de Gibbs-Duhem établissent une relation entre pression, température et potentiels chimiques. Ces paramètres d'état intensifs ne sont donc pas indépendants. Dans le cas du corps pur, le potentiel chimique peut être directement calculé en fonction de
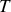et
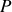à partir d'une relation de Gibbs-Duhem, comme l'illustre l'exemple du corps idéalement incompressible.
Exemple :
Considérons le cas idéal d'un corps pur incompressible, de volume molaire
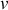. Ce volume invariable est égal à la dérivée partielle
d'après l'équation (47). Par intégration à température constante par rapport à la pression, il vient
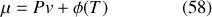
où la fonction d'intégration
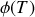(analogue à la constante d'intégration des fonctions à une seule variable) est telle que :
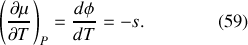
Or, la différentielle de l'entropie molaire du corps incompressible est, en fonction de la capacité thermique molaire
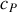et de
:
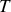En effet, le coefficient thermique
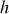est proportionnel à une dérivée du volume comme le montre la relation de Clapeyron (32). Il est donc nul pour un corps incompressible. La différentielle de
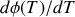est ainsi donnée par
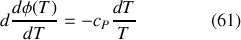
et le potentiel chimique du corps pur incompressible peut être écrit sous la forme
