Soit un gaz parfait pur, de volume molaire
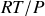 . D'après l'équation (47) :
. D'après l'équation (47) :
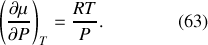
Par intégration, il vient
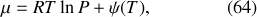
où la fonction d'intégration
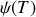 dépend en partie de l'unité choisie pour exprimer la pression.
dépend en partie de l'unité choisie pour exprimer la pression.
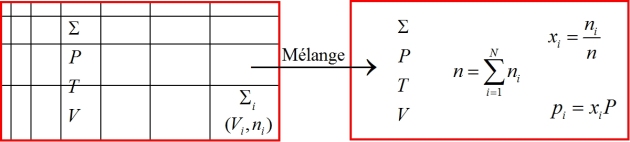
Cherchons maintenant à définir le potentiel chimique d'un gaz parfait dans un mélange de
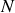 gaz parfaits qui n'interagissent pas entre eux, un mélange
gaz parfaits qui n'interagissent pas entre eux, un mélange « idéal »
.
Considérons dans un premier temps un système isolé
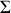 de volume
de volume
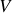 constitué de
constitué de
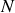 sous-systèmes cloisonnés
sous-systèmes cloisonnés
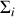 de volumes
de volumes
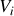 . Dans chacun des sous-systèmes
. Dans chacun des sous-systèmes
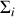 ,
,
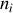 moles du gaz pur
moles du gaz pur
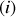 sont à l'équilibre thermomécanique à la température
sont à l'équilibre thermomécanique à la température
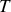 et à la pression
et à la pression
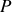 . Les gaz
. Les gaz
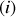 étant supposés parfaits, ils vérifient les
étant supposés parfaits, ils vérifient les
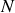 relations
relations

et possèdent tous un potentiel chimique de la forme
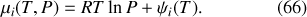
Dans un second temps, les cloisons disparaissent. Les gaz se mélangent et finissent tous par occuper le volume total
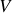 . Le mélange étant idéal, les molécules d'un gaz parfait
. Le mélange étant idéal, les molécules d'un gaz parfait
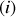 n'interagissent pas plus avec les molécules des autres gaz parfaits qu'elles n'interagissent entre elles. La température finale ne doit donc pas être différente de la température initiale (l'énergie interne
n'interagissent pas plus avec les molécules des autres gaz parfaits qu'elles n'interagissent entre elles. La température finale ne doit donc pas être différente de la température initiale (l'énergie interne
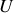 de
de
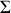 restant constante par ailleurs). La pression partielle
restant constante par ailleurs). La pression partielle
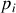 de chacun des gaz du mélange à l'état final vérifie par conséquent :
de chacun des gaz du mélange à l'état final vérifie par conséquent :
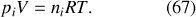
De plus, si n désigne le nombre total de moles du mélange idéal, la loi du gaz parfait s'énonce sous la forme

En divisant chaque terme des équations (65) et (67) par le terme correspondant de l'équation (68), on obtient les égalités
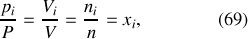
où
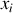 désigne la
désigne la « fraction molaire »
(ou « titre »
) du gaz
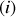 .
.
Si aucune variation d'énergie n'accompagne le mélange, il n'en est pas de même pour l'entropie. La différentielle de l'entropie molaire d'un gaz parfait est en effet donnée par
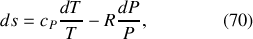
À l'issue du mélange isotherme, la variation d'entropie d'un gaz parfait
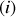 est strictement positive (la fraction molaire
est strictement positive (la fraction molaire
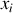 étant plus petite que un) :
étant plus petite que un) :
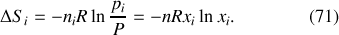
La variation positive d'entropie du système global
 s'exprime en conséquence par
s'exprime en conséquence par
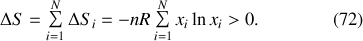
Or, la variation d'enthalpie libre de
 se déduit directement de cette variation d'entropie. En effet, les fonctions
se déduit directement de cette variation d'entropie. En effet, les fonctions
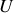 ,
,
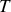 et
et
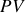 restent constantes au cours du mélange et
restent constantes au cours du mélange et
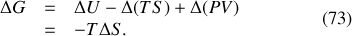
Par suite, et c'est là le résultat naturel de l'évolution du système vers son état le plus probable, le potentiel thermodynamique
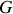 a diminué au cours du mélange idéal des différents gaz parfaits du système :
a diminué au cours du mélange idéal des différents gaz parfaits du système :
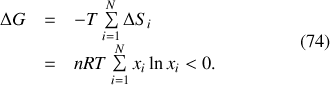
Ainsi l'enthalpie libre à l'état final est-elle donnée par
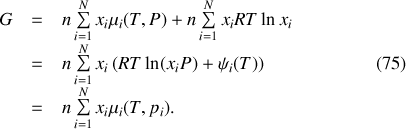
La définition (64) du potentiel chimique du gaz parfait est reconduite pour le gaz parfait mélangé idéalement à d'autres gaz parfaits, à la condition expresse que la pression considérée dans cette définition soit la pression partielle
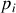 du gaz étudié :
du gaz étudié :
Conclusion
En définissant un potentiel chimique du gaz parfait dans l'état pur de référence
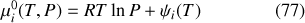
le potentiel chimique d'un gaz parfait d'un mélange idéal de gaz parfait peut être exprimé sous la forme
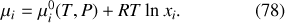
Attention :
Le potentiel chimique du gaz parfait d'un mélange idéal de gaz parfaits est souvent défini par rapport à une pression de référence
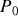 . Dans ce cas, le potentiel de référence ne dépend que de la température
. Dans ce cas, le potentiel de référence ne dépend que de la température
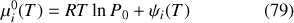
et le potentiel chimique prend la forme
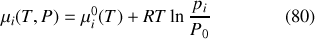
Remarque :
La fonction d'intégration
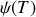 d'un gaz parfait est telle que sa dérivée vérifie :
d'un gaz parfait est telle que sa dérivée vérifie :
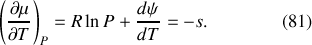
La différentielle
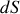 de l'entropie molaire d'un gaz parfait étant donnée par l'équation (70), celle de
de l'entropie molaire d'un gaz parfait étant donnée par l'équation (70), celle de
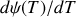 l'est par
l'est par
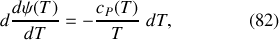
et la fonction
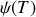 peut être calculée à partir de la double intégrale
peut être calculée à partir de la double intégrale
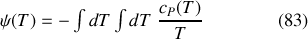
dès lors que la loi de variation de la capacité thermique avec la température est connue. Il faut souligner qu'un tel calcul devient plus compliqué dans le cas de corps réels. En effet, ceux-ci subissent des transitions de phase et possèdent des capacités thermiques différentes dans chacun de leurs états.