Le nombre 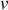de paramètres d'état indépendants d'un système est nommé « variance ». Il est égal au nombre 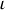de paramètres intensifs du système diminué du nombre 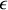d'équations d'état indépendantes qui relient entre eux ces paramètres.

Pour un corps pur existant dans une phase donnée, il y a trois paramètres d'état intensifs : 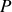, 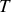et le volume molaire 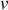. L'équation d'état du corps permet d'exprimer l'un de ces trois paramètres en fonction des deux autres (pour un gaz parfait, par exemple, 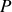est égal à 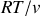). Or, c'est la seule équation reliant les trois paramètres. Une phase donnée d'un corps pur a donc deux paramètres d'état indépendants.

Lorsque 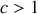corps purs et/ou 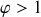phases coexistent au sein d'un même système fermé, la variance ne peut plus se résumer aux deux paramètres d'état indépendants d'une phase unique de corps pur. Toutefois, la variance peut être exprimée en fonction de 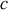et .

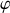Calculons dans un premier temps le nombre 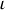de paramètres intensifs en fonction de 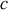et 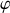. Une quantité molaire 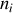(ou massique 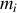) de molécules caractérise la présence d'un corps pur 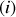. De même, une quantité 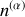(ou 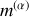) de molécules signe l'existence d'une phase ( 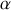). Prenant le rôle que joue le volume molaire dans le cas du corps pur, la fraction molaire (ou massique)

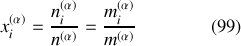
est un paramètre intensif qui définit la proportion du constituant 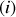en phase ( 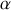) relativement à la quantité de matière existant en phase ( 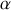). Il existe en tout 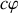fractions molaires, puisqu'il existe 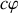manières de grouper les 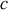indices 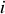et les 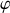superindices ( 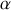). Il faut ajouter à ce nombre celui des deux paramètres intensifs extérieurs indépendants 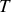et 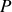qui déterminent l'état de tous les corps purs 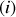en phase ( 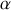). En effet, les températures et pressions des divers corps et des diverses phases sont toutes égales à l'équilibre. Par suite :

Considérons dans un second temps le nombre 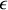d'équations reliant les paramètres d'état en fonction de 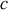et 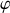. À l'équilibre du système, pour chaque constituant, il y a égalité des potentiels chimiques caractérisant une phase ( 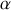) pour chaque constituant 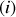. On a donc 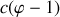égalités du type :

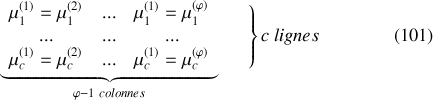
De plus, pour chaque phase ( 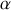), il est possible d'exprimer une fraction molaire de constituant (par exemple le constituant 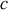) en fonction des 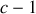autres car

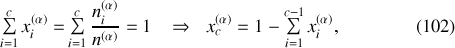
et il existe 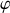égalités de ce dernier type. Le nombre total d'équations est donc :

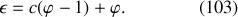
La variance étant égale à la différence entre 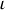et 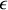, on en déduit immédiatement la « règle des phases » établie en 1876 par Willard Gibbs :

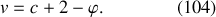
Pour les corps purs ( 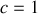), cette règle des phases permet de :

• retrouver la divariance ( 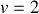) constatée pour la phase homogène ( ) ;

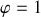• prévoir que la coexistence de deux phases ( 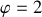) à l'équilibre définit un système monovariant ( 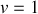) où la température (de transition de phase) dépend de la pression et dessine une courbe (dite de « pression saturante ») dans un espace ( , ) ;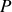

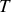• deviner qu'il existe dans ce même espace ( 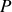, 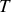) un point triple ( 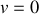) où les trois phases solide, liquide et vapeur coexistent.

Mais c'est pour les mélanges de plusieurs corps que la règle des phases est la plus utile.