Considérons une fonction d'onde bâtie à partir de deux fonctions d'onde individuelles :
Attention : cette fonction d'onde ainsi composée, sans pour autant forcément décrire exactement la réalité, n'est donc pas un produit de fonctions d'onde individuelles qui serait une approximation encore plus mauvaise ! Pour plus de détails, se référer aux chapitres concernant la méthode de Hartree-Fock et ses extensions dans le cours de physique/chimie quantique ou de modélisation microscopique de la matière.
Soit ![]() : fonction de permutation
: fonction de permutation
on a donc:
Si on considère deux niveaux (2 électrons) :
si ![]() alors
alors ![]() ce qui est inacceptable vu l'exigence de normalisation des probabilités de présence dans l'espace entier.
ce qui est inacceptable vu l'exigence de normalisation des probabilités de présence dans l'espace entier.
C'est le principe de Pauli, qui stipule que deux électrons ne peuvent pas occuper la même configuration quantique (si on tient compte des spin +1/2 et -1/2).
On peut établir l'expression du poids W d'une conformation en tenant en plus compte de la dégénérescence éventuelle ![]() d'un niveau (c'est à dire qu'on peut classer les niveaux par
d'un niveau (c'est à dire qu'on peut classer les niveaux par « numéro »
, mais regrouper les niveaux de même énergie sous la même étiquette ; dans le cas de l'atome d'hydrogène, en première approximation, le niveau ![]() est dégénéré
est dégénéré ![]() fois.
fois.
Dans le cas des Boltzmannions (particules discernables), l'expression du poids W s'écrit :
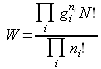
Dans le cas des Fermions, l'expression du poids W s'écrit :
Dans le cas des Bosons, l'expression du poids W s'écrit :
Considérons l'exemple de deux particules à répartir sur deux configurations quantiques d'énergie 0 et ![]() non dégénérées.
non dégénérées.
Dans le cas des Boltzmannions, toutes les possibilités sont autorisées, et il y a deux façons, les particules étant discernables, d'obtenir l'énergie , et une seule façon d'obtenir les énergies 0 et
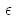 .
.
Dans le cas des Fermions, une seule possibilité est autorisée si on ne veut pas que deux particules soient sur le même niveau.
Pour les Bosons, toutes les possibilités sont autorisées mais les particules étant indiscernables il n'y a qu'une seule façon d'obtenir l'énergie
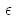 .
.
Résumons les valeurs de la fonction de partition ![]() dans ces trois cas :
dans ces trois cas :
Deux boltzmannions :
dans ce seul cas la factorisation est possible.
Deux fermions :
Deux bosons :
ici ![]() .
.
Formule générale
Pour les Boltzmannions :
comme déjà vu et constaté sur l'exemple.
Pour les Fermions ou les Bosons la fonction de partition canonique est difficilement exprimable sous forme de produit, mais en passant dans l'ensemble grand canonique la grande fonction de partition vaut :
avec ![]() .
.
en permutant somme et produit,
Dans le cas des bosons
![]() va de 0 à l'infini puisque toutes les conformations quantiques sont autorisées.
va de 0 à l'infini puisque toutes les conformations quantiques sont autorisées.
(on reconnaît la somme d'une progression géométrique).
Le nombre moyen de particules vaut ![]() comme vu dans le chapitre sur le grand-canonique , donc :
comme vu dans le chapitre sur le grand-canonique , donc :
d'où :
Dans le cas des fermions
![]() ne peut valoir que 0 ou 1 vu le principe d'exclusion de Pauli donc la fonction de partition s'écrit sous la forme :
ne peut valoir que 0 ou 1 vu le principe d'exclusion de Pauli donc la fonction de partition s'écrit sous la forme : ![]() .
.
Par conséquent le nombre moyen de particules est :
d'où :
Le nombre moyen de particules sur un niveau
Le nombre moyen de particules sur un niveau est donné par :
Dans le cas des fermions on a :
et dans le cas des bosons on a :
En factorisant on obtient le facteur quantique :
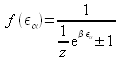
ou :
« + »
dans le cas des fermions et « - »
dans celui des bosons
Dans le cas des bosons, on parle de la distribution de Bose-Einstein (1924)
Dans le cas des fermions, on parle de la distribution de Fermi-Dirac (1926)
si ![]() alors le facteur quantique vaut environ
alors le facteur quantique vaut environ ![]()
donc on retrouve la distribution de Boltzmann dans les deux cas.
Dans le cas de la distribution de Fermi-Dirac le facteur quantique peut également s'écrire sous la forme :
avec ![]() et
et ![]() appelé
appelé « Energie de Fermi »
, identifiée au potentiel chimique, et correspondant à l'énergie du dernier électron « empilé »
à température nulle.
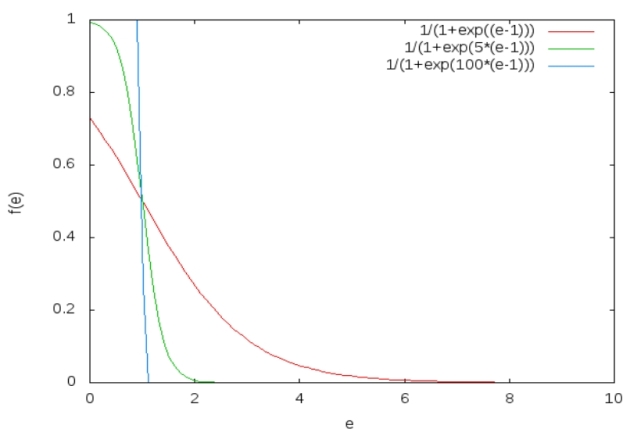
* Représentation de la variation du facteur quantique de Fermi-Dirac en fonction de ![]() pour différentes températures (ou valeurs de
pour différentes températures (ou valeurs de ![]() ) pour une énergie de Fermi de 1 en unités arbitraires. On voit qu'aux basses températures on passe rapidement d'un facteur 1 à un facteur 0 autour de l'énergie de Fermi, et qu'aux températures élevées on se rapproche d'un facteur de Boltzmann (exponentielle décroissante)
) pour une énergie de Fermi de 1 en unités arbitraires. On voit qu'aux basses températures on passe rapidement d'un facteur 1 à un facteur 0 autour de l'énergie de Fermi, et qu'aux températures élevées on se rapproche d'un facteur de Boltzmann (exponentielle décroissante)
Dans le cas où les particules sont des bosons le facteur quantique s'écrit sous la forme :
Pour les fermions, si la température ![]() alors
alors ![]() , donc : si
, donc : si ![]() alors
alors ![]() .
.
On a défini la fugacité de la molécule par ![]() .
.
si ![]() alors
alors ![]() et
et ![]() .
.
On retrouve la distribution de Maxwell-Bolzmann.
Le nombre moyen des particules s'écrit :
Pour le gaz parfait, la fonction de partition microcanonique ![]() vaut :
vaut :
avec ![]() longueur d'onde de de Broglie comme déjà vu. Alors :
longueur d'onde de de Broglie comme déjà vu. Alors :
avec ![]() densité volumique de particules.
densité volumique de particules.
La condition ![]() donne
donne ![]() .
.
On définit la température de dégénérescence par :
avec ![]()
d'où :
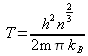
Exemple :
On considère le cas de l'hélium dont le paramètre de maille est ![]() . On trouve que la température de dégénérescence vaut
. On trouve que la température de dégénérescence vaut ![]() et la longueur d 'onde thermique
et la longueur d 'onde thermique ![]() .
.
La grande fonction de partition vaut :
avec ![]() fonction de partition dans l'ensemble canonique.
fonction de partition dans l'ensemble canonique.
On suppose que ![]() soit
soit ![]() et
et ![]()
avec (+) dans le cas des fermions et (-) dans le cas des bosons.
On suppose que ![]() d'où
d'où ![]() en développant le logarithme au premier ordre.
en développant le logarithme au premier ordre.
Or ![]() donc
donc ![]()
d'autre part ![]() donc
donc ![]() , or
, or ![]() donc :
donc : ![]() .
.
Comme ![]() ,
,
d'où ![]() et donc :
et donc :
comme annoncé dans le chapitre sur l'ensemble canonique.
![]() diminue du fait que les particules sont indiscernables
diminue du fait que les particules sont indiscernables
En poursuivant le développement du logarithme de la grande fonction de partition :
avec (+) pour les fermions et (-)pour les fermions.
Dans le cas du gaz parfait :
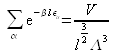
en reprenant le calcul de la fonction de partition avec un ![]() supplémentaire dans l'intégrale.
supplémentaire dans l'intégrale.
Nous obtenons pour le nombre moyen de particules :