Pour le gaz parfait en calculant la densité numérique on obtient :
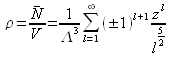
En s'arrêtant à l'ordre
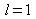de ces développements (pour 
et pour sa dérivée) on obtient :
Donc : 
et 
or, 
par définition de la pression dans l'ensemble grand-canonique.
Finalement :
alors : 
, 
avec 
nombre de moles.
Donc 
à l'ordre 1, on retrouve la relation des gaz parfaits.
A l'ordre
:
donc :
d'où :
Donc :
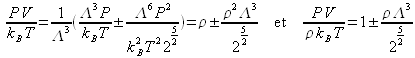
(+) pour les fermions et (-) pour les bosons.
Si les particules sont quantiques, il y a une correction de la pression par rapport à la loi usuelle des gaz parfaits classiques, même dans le cas d'un gaz parfait quantique. On retrouve une répulsion des fermions et une attraction des bosons.
Pour un système dégénéré, il faut tenir compte de la densité d'état : 
.
Le nombre de particules total vaut donc :
Pour un gaz parfait non-relativiste, nous avons vu que la densité d'état est donnée par :
avec 
le spin de la particule et 
.
Généralisation de l'expression
* de 
.
b=0 : Maxwell Boltzmann, b=1 : Fermi – Dirac, b=-1 : Bose – Einstein
Pour les électrons (fermions) à température nulle (où le potentiel chimique s'identifie à l'énergie de Fermi) on trouve donc :
alors :
avec 
la densité du système.
On constate que l'énergie de Fermi est une fonction de la densité électronique ; la théorie dite de la « fonctionnelle de la densité »
, très utilisée aujourd'hui en physique et chimie quantique, procède d'une généralisation de ce type de remarque dans le cas des gaz de fermions réels.
Revenons au cas des bosons ; le nombre total de particules peut être divisé en :
: nombre de particules dans l'état fondamental où manifestemennt une divergence se produit au numérateur de l'expression (condensat de Bose-Einstein).
dans le cas du gaz parfait non-relativiste.
On pose :
alors :
donc :
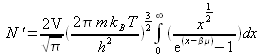
On définit une nouvelle fonction 
telle que :
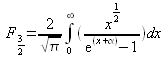
avec 
. Donc :
(résultat obtenu par calcul numérique).
D'où :
est proportionnel à 
.
En dessous de la température critique 
, 
va commencer à augmenter pour satisfaire 
.
Exemple : - cas de l'hélium
Si 
, 
En pratique on mesure 
et on trouve que 
donc cette théorie approximative (hypothèse du gaz parfait) donne un résultat tout de même satisfaisant.
Calcul de l'énergie interne U
On pose :
d'où l'énergie interne :
tel que :
or 
. D'autre part :
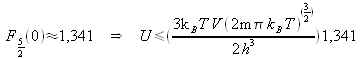
Calcul de la capacité calorifique
L'énergie maximale est donnée par :
Or :
donc :
Donc :
et on obtient une capacité calorifique qui tend vers 0 quand la température tend vers 0, sans pour autant qu'il y ait le même type de discontinuité à la température critique que dans une transition de phase dite du « premier ordre »
(telle que la fusion de l'eau) où la capacité calorifique présente une discontinuité correspondant à la chaleur latente de fusion.
