Comme nous l'avons déjà vu la fonction de partition s'écrit en trois dimensions (en négligeant les degrés de liberté de rotation, vibration, électroniques)
avec ![]() le nombre d'atomes ou de molécules et :
le nombre d'atomes ou de molécules et :
avec ![]() l'énergie potentielle d'interaction des atomes.
l'énergie potentielle d'interaction des atomes.
Dans le cas du gaz parfait ![]() et cette intégrale se réduit au volume donc
et cette intégrale se réduit au volume donc ![]() . La seule contribution au Hamiltonien du gaz parfait est le terme d'énergie cinétique qui donne le terme en
. La seule contribution au Hamiltonien du gaz parfait est le terme d'énergie cinétique qui donne le terme en ![]() que nous avons déjà vu.
que nous avons déjà vu.
Il est à noter que ![]() dépend de toutes les coordonnées des atomes simultanément.
dépend de toutes les coordonnées des atomes simultanément.
Par exemple, dans le cas de métaux, on a des électrons de valence quasi-libres qui participent tous à la conductivité électrique et thermique et assurent la liaison chimique. (Notons qu'on voit ces électrons former un plasma à la surface du métal. Ce plasma étant opaque à certaines fréquences électromagnétiques, on voit alors apparaître l'éclat métallique si la surface du métal n'est pas oxydée).
Pour les isolants (systèmes ioniques, covalents, gaz rares...), on peut décomposer ![]() en plusieurs potentiels à 2 corps, 3 corps, etc, modélisant la liaison entre atomes ou molécules (tenant compte par exemple de l'orientation relative de deux molécules telles que l'eau)
en plusieurs potentiels à 2 corps, 3 corps, etc, modélisant la liaison entre atomes ou molécules (tenant compte par exemple de l'orientation relative de deux molécules telles que l'eau)
en excluant la somme sur ![]() .
.
La plupart du temps on se limite cependant dans la modélisation à des potentiels à deux corps, par exemple électrostatiques dans le cas de systèmes ioniques, avec un terme répulsif exponentiel du type « Born-Mayer »
pour empêcher une contraction totale d'un potentiel purement attractif.
Dans le cas des gaz rares tels que Ne; Ar ;Kr (ni trop légers comme l'hélium pour exiger un traitement quantique, ni trop lourds pour exiger un traitement relativiste des électrons).
![]() peut s'écrire sous la forme :
peut s'écrire sous la forme :
(on divise le terme par 2 pour ne pas compter doublement les interactions de l'atome ![]() avec l'atome
avec l'atome ![]() , ou on se limite à une somme pour
, ou on se limite à une somme pour ![]() )
)
On choisit souvent le potentiel dit de Lennard-Jones :
qui a un bon pouvoir descriptif pour ces systèmes, et présente des régularités analytiques permettant de facilement le dériver, par exemple, contrairement à des potentiels dits de sphères dures. On remarque que ce potentiel présente une partie attractive à longue distance correspondant à une modélisation de l'interaction dipôle-dipôle entre atomes neutres (en ![]() ) et un terme répulsif à courte distance, la somme des deux permettant de prévoir une distance d'équilibre entre atomes et des phénomènes tels que la liquéfaction du gaz à température suffisamment basse.
) et un terme répulsif à courte distance, la somme des deux permettant de prévoir une distance d'équilibre entre atomes et des phénomènes tels que la liquéfaction du gaz à température suffisamment basse.
On introduit alors la fonction de distribution radiale ![]() qui va nous permettre de calculer dans l'ensemble canonique le nombre de paires d'atomes moyen à la distance
qui va nous permettre de calculer dans l'ensemble canonique le nombre de paires d'atomes moyen à la distance ![]() l'un de l'autre :
l'un de l'autre :
avec la densité numérique :
La moyenne est calculée comme dans les chapitres précédents à partir d'un facteur de Boltzmann ; les contributions cinétiques à l'énergie se compensent au dénominateur et nominateur et on obtient :
Remarquons que tous les ![]() termes de la somme sont identiques au premier et que donc :
termes de la somme sont identiques au premier et que donc :
En remarquant que le potentiel dans le cas des gaz rares ne dépend que de la distance mutuelle entre deux atomes ![]() , on peut simplifier les deux premières intégrales et obtenir en décalant l'origine en
, on peut simplifier les deux premières intégrales et obtenir en décalant l'origine en ![]() puis en posant
puis en posant ![]() .
.
On rappelle que la pression du gaz s'exprime dans l'ensemble canonique par :
Or pour un gaz parfait la fonction de partition vaut :
donc :
et on retrouve la loi macroscopique des gaz parfaits ![]() .
.
Pour un gaz réel, la fonction de partition est :
donc :
or :
Remarquons qu'en changeant de variable afin d'intégrer explicitement sur le volume ![]() , c'est à dire en posant :
, c'est à dire en posant :
on obtient :
En posant ![]() :
:
et dérivant par rapport à ![]() on obtient donc :
on obtient donc :
en revenant aux variables dimensionnées et avec ![]()
or :
Dans la première équation on peut tout ramener à une intégration sur ![]() et on obtient :
et on obtient :
donc, comme :
en dérivant le logarithme on a deux simplifications et :
en supposant que ![]() et en introduisant
et en introduisant ![]() , on obtient :
, on obtient :
Rappelons nous de l'expression de la fonction de densité de paires :
donc :
Si le gaz n'est pas parfait mais tout de même dilué, seules les interactions de paires vont intervenir dans la moyenne :
avec :
et finalement ne demeure que ![]() en supposant que la probabilité de trouver une paire à la distance
en supposant que la probabilité de trouver une paire à la distance ![]() est donnée par un facteur de Boltzmann. La normalisation de la fonction de densité de paires est manifestement correcte.
est donnée par un facteur de Boltzmann. La normalisation de la fonction de densité de paires est manifestement correcte.
En utilisant cette formule, en reprenant l'expression de la pression puis par une intégration par parties :
Si ![]() on trouve bien le cas du gaz parfait.
on trouve bien le cas du gaz parfait.
Exemple : - le gaz de sphères dures
![]() pour
pour ![]()
![]() pour
pour ![]()
or ![]() , donc :
, donc :
soit en écrivant :
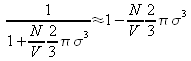
en développant au premier ordre :
ou encore :
avec ![]() demi-volume exclu des
demi-volume exclu des ![]() sphères dures.
sphères dures.
On retrouve donc bien l'équation de Van der Waals simplifiée dans ce cas, et nous avons fait le lien entre vision microscopique et macroscopique. On pourrait trouver le reste de l'équation en tenant compte d'une partie attractive du potentiel.



