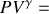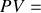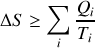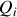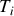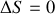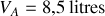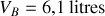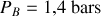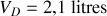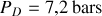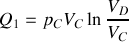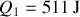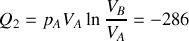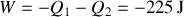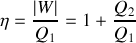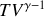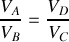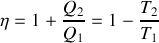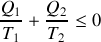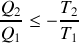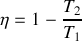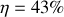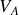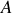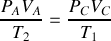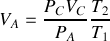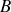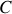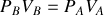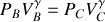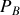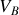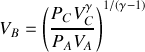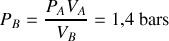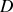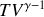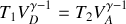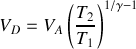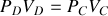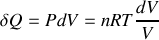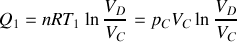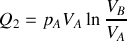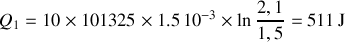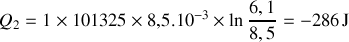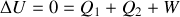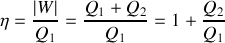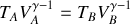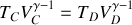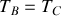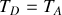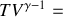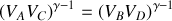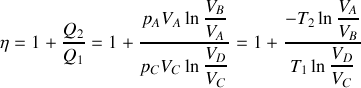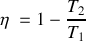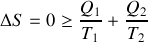Énoncé
Un gaz diatomique subit un cycle de transformations quasi-statiques dithermes dit de Carnot :
soit (i) la succession d'une compression isotherme AB à la température
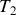 , (ii) une compression adiabatique BC, (iii) une détente isotherme CD à la température
, (ii) une compression adiabatique BC, (iii) une détente isotherme CD à la température
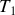 , et enfin (iv) une détente adiabatique
, et enfin (iv) une détente adiabatique
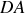 . Les données sont les suivantes :
. Les données sont les suivantes :
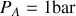 et
et
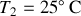 ;
;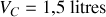 et
et
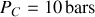 ,
,
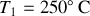 ;
;pour un gaz diatomique,
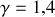 .
.
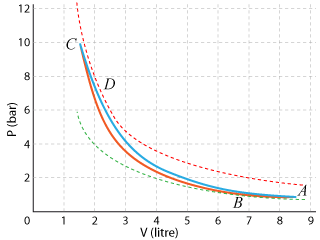
Déterminer les coordonnées dans un diagramme
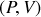 des quatre points du cycle.
des quatre points du cycle.Tracer le cycle dans le diagramme de Clapeyron (échelle des abscisses : 2 cm pour 1 litre; échelle des ordonnées : 1 cm pour 1 bar).
Calculer les quantités de chaleur
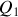 et
et
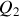 et le travail
et le travail
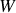 reçus par le gaz au cours du cycle et préciser leurs signes. De quelle type de machine thermique s'agit-il ?
reçus par le gaz au cours du cycle et préciser leurs signes. De quelle type de machine thermique s'agit-il ? Donner les expressions de l'efficacité
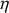 de cette machine dithermique en fonction de
de cette machine dithermique en fonction de
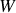 ,
,
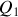 et
et
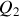 , puis en fonction des températures
, puis en fonction des températures
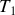 et
et
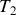 en remarquant la relation liant les volumes des quatre points du cycle.
en remarquant la relation liant les volumes des quatre points du cycle. Quel principe permet de retrouver cette dernière expression pour
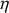 ?
?Calculer cette efficacité.