Les trois principes fondateurs (Lois de la mécanique de Newton ou formalisme vectoriel) peuvent être résumés ainsi :
Fondamental :
1) Principe d'inertie :
Dans un référentiel galiléen, un système isolé a un mouvement rectiligne uniforme.
La version originale d'Isaac Newton : « Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui et ne le contraigne à changer d'état. »
La version originale est à rapprocher du second principe ci- après, où nulle indication à la notion de référentiel galiléen n'est présente.
2) Principe fondamental de la dynamique (ou PFD).
Ce principe vectoriel associe d'une part,
la variation de la quantité de mouvement ou (impulsion)
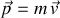, ou encore l'accélération
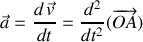
à d'autre part,
la résultante
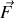des forces appliquées sur le point matériel
.
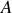Énoncé :
Dans un référentiel galiléen, la résultante des forces appliquées produit une variation de quantité de mouvement au cours du temps telle que :
.
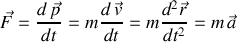Les 3 dernières égalités sont valides si la masse du système étudié est constante.
Ce postulat fournit les équations vectorielles du mouvement.
3) Principe de l'action et de la réaction ou principe des actions réciproques,
à l'origine des forces de contact et de liaison, pouvant s'effectuer à distance.
Exprimé dans sa version originale, il s'énonce ainsi :
« Tout corps
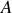exerçant une force sur un corps
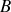subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps
».
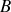Dans sa formulation mathématique, il s'écrit :
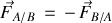
Ce dernier principe nécessite de délimiter spatialement le système étudié.
Aux points de contact avec le milieu extérieur s'exercent des réactions aux forces appliquées (actions).
À l'intérieur du système, actions et réactions (internes) s'annulent.
Ainsi, pour un solide en équilibre, la résultante des forces appliquées doit être nulle.
Ce bilan de forces n'inclut pas les forces internes lesquelles s'annulent 2 à 2.
De même lors de l'interaction gravitationnelle à deux corps, chacun des corps pris séparément est soumis à l'attraction de l'autre (une force à distance).
En considérant l'ensemble des deux corps, le système obtenu est isolé : les forces qui s'appliquent deviennent internes et s'annulent.
Quelques remarques, rappels et compléments peuvent être précisés, sans être exhaustif.
Explication : La vitesse entre dérivée et valeur moyenne
Les 2 éléments cinématiques associés au mouvement, vitesse et accélération (sous-entendu instantanées) utilisent la notion de dérivée par rapport au temps.
En physique expérimentale, les mesures conduisent à des notions de vitesse et accélération moyennes entre les deux points de mesure.
Cette moyenne est assujettie à la précision de mesure sur le temps : l'intervalle
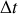entre les deux mesures qui influe sur la distance parcourue.
Cet intervalle est tributaire de la méthode de mesure et surtout de l'appareillage.
Ainsi le vecteur-vitesse moyenne entre deux points
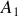et
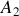est calculé selon :
.
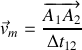Son module correspond au rapport du segment
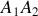sur la durée du déplacement,
son point d'application est le milieu du segment
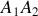et
sa direction est celle du segment, dans le sens du mouvement.
La vitesse moyenne
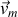sera d'autant plus proche de la vitesse instantanée
que l'intervalle
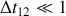; ceci correspond au sens physique de la limite
.
La vitesse instantanée est définie par la dérivée :
.
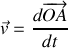Sa représentation graphique est la tangente à l'arc
.
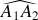Complément : Qu'est-ce qu'une force ?
- C'est un vecteur caractérisé par une amplitude, une direction, un sens et un point d'application.
Ce dernier élément sera prépondérant avec la notion de moment de force et la rotation qu'il décrit (voir le paragraphe C de ce chapitre).
Cette description vectorielle entraîne toutes les notions sous-jacentes de symétrie (propriété de l'espace) ou plus interactives comme le champ, perceptible par son effet : chaque notion a une interprétation en physique.
- La mécanique physique définit la force comme un élément contribuant à l'équilibre ou au mouvement des corps.
L'échelle adossée au mur peut être soit en équilibre soit en mouvement et les forces sont à l'origine des deux situations. Certes par leurs intensités, leurs directions, sens et points d'application, leur nature étant vectorielle.
Parmi les différents types de forces connues, elle peut être :
Gravitationnelle avec le cas particulier du poids (champ gravitationnel et champ de pesanteur).
électrostatique ou force électrique (champ électrique),
magnétique.
Leur action à distance permet une description en termes de propriétés de l'espace ou champ.
Élastique issue d'un ressort ou d'un élastique (avec la notion d'équilibre sous-jacente) dont l'action et le point d'application sont localisés dans l'espace.
Cette action caractérise également un comportement au voisinage de tout point d'équilibre.
Le frottement, visqueux (proportionnel à la vitesse) ou dur (ou solide) ou tout autre forme de résistance au mouvement.
Celles de contact entre les corps, qui peut être direct, ou de cohésion et/ou de liaison qui dépendent et sont modifiées par le mouvement...
Une nébuleuse qui nécessite un traitement à part.
Et ne relevant pas de ce cours de mécanique classique, les forces de cohésion nucléaires.
Toute force, hors forces de contact d'équilibre, produit un déplacement.
Elle est ainsi caractérisée par une grandeur scalaire mesurant le travail effectué pendant le déplacement.
Cette notion, associant force et déplacement, existe pendant le mouvement et peut être favorable (moteur) ou défavorable (freinant) au mouvement.
Définition : Travail d'une force
Le travail d'une force pendant un déplacement élémentaire est le produit scalaire entre la force et le déplacement qu'elle produit ou freine.
Le travail en équation.
Entre deux points
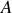et
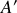, très proches, permettant d'assurer une force constante pendant le déplacement, le travail est donné par la relation :
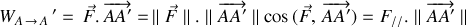
La composante "algébrique" de
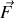projetée sur l'axe du déplacement est notée
.
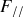Le signe de l'expression est porté par l'angle et son cosinus : il indique un travail positif (donc reçu et moteur) ou négatif (et résistant).
Ainsi le travail existe, est efficace (donc non nul) si force et déplacement sont simultanément non nuls et non orthogonaux : seule la composante parallèle au déplacement travaille (déduit de la définition du produit scalaire).
La force orthogonale au déplacement
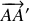n'est pas 'efficace' sur ce déplacement : le mouvement qu'elle produit a lieu selon la direction perpendiculaire à
.
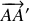Complément : Qu'est ce qu'un mouvement ?
Le mouvement correspond à l'existence d'un déplacement.
Mais à l'aune des postulats il existe un déplacement qui joue un rôle particulier : celui où la résultante des forces est nulle.
Avec le principe d'action et de réaction, une résultante des forces nulle suggére une situation d'équilibre et d'absence de mouvement.
Selon le PFD et en l'absence de forces (résultante nulle),
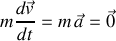. Si l'accélération du point matériel est nulle, le vecteur-vitesse est un vecteur constant (en amplitude, direction et sens, tous trois imposés par la condition initiale), dont le vecteur vitesse nul.
Le principe d'inertie a une réponse plus directe puisque le point matériel isolé (dont la résultante des forces est nulle) est en mouvement rectiligne avec une vitesse uniforme, qui peut être nulle.
Il apparaît un mouvement particulier, rectiligne à vitesse uniforme, d'un coté et ... tous les autres types de mouvement de l'autre.
Ce rôle particulier de mouvement rectiligne à vitesse uniforme est à l'origine de la notion de référentiel galiléen.
Mais des compléments précisant les principes énoncés ci-dessus, un mouvement particulier et ses éléments de description sont nécessaires à la mise en place des référentiels galiléens et non galiléens (chapitre 3).
Attention : Application des postulats et définition du système mécanique.
Les limites du système à étudier doivent être précisées surtout lorsque plusieurs particules, ou groupes de particules, participent au mouvement (comme la machine d'Atwood), ou lorsque des contacts et interactions avec l'extérieur ont lieu (échelles contre un mur, échafaudage d'échelles, gaz dans une enceinte...).
Dans une même étude, il peut être utile de considérer simultanément chaque particule ou une partie ou l'ensemble : le principe d'action et de réaction s'adapte alors à chaque situation.
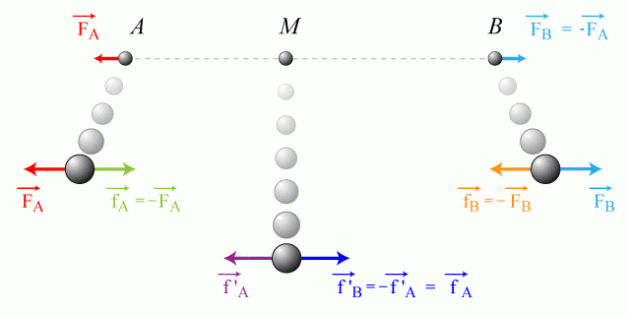
Ainsi l'équilibre obtenu en tirant de part et d'autre d'une corde inextensible d'extrémités
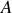et
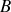(fig. 4) s'explique globalement par l'annulation des deux forces (extérieures
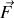) appliquées aux extrémités.
Mais considérant chaque extrémité séparément, chaque force extérieure est directement compensée par la traction (réaction locale
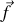) de la corde. Ce continuum de forces de réaction de la corde est présent tout au long et en tout point, à l'exemple du point matériel
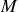isolé sur la fig. 4. Il disparaît dans une description de l'ensemble car ces forces deviennent internes et se neutralisent mutuellement dans le système complet. Leur existence s'avère lorsque la corde casse.
