L'application du PFD à un système en mouvement nécessite un bilan des forces.
Certaines sont systématiques, "visibles", comme les interactions extérieures précédemment répertoriées : gravitationnelle ou de pesanteur, électrostatique, magnétique, élastique...
Les points de contact avec le milieu extérieur peuvent présenter des frottements ou non, mais les composantes des forces de contact sont quelquefois peu explicites, surtout celles qui apparaissent avec le mouvement et sous des contraintes.
Les deux exemples suivants sont aisés à appréhender.
Ils sont élaborés à partir de contraintes, géométrique ou pouvant avoir une origine extérieure et permettent de construire une approche progressive du bilan des forces.
Exemple : 1. Mouvement d'une bille dans une glissière circulaire horizontale
Le mouvement de la bille, de masse
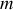, est soumis à la contrainte de forme de la glissière : il sera donc circulaire de rayon
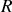. (fig. 5)
La cinématique permet de déduire :
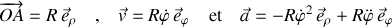
Un seul degré de liberté (variable) se dégage pour décrire le mouvement de la bille : l'angle
des coordonnées polaires et tel que
.
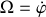L'accélération a deux composantes.
Méthode : Analyse en termes de forces
D'après le PFD (ou accélération = force/masse), une analyse systématique en termes de composantes des forces conduit aux points suivants.
La résultante des forces doit posséder
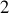composantes : l'une radiale et dirigée vers le centre
(centripète), l'autre est tangente au cercle formé par la glissière.
Le poids de la bille, selon l'axe
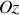, n'apparaît pas. Il est directement compensé par "une partie" de la "réaction" du support : la glissière.
La résultante radiale ne peut trouver son explication que dans le contact bille-glissière : une composante de la réaction du support qui n'est plus seulement verticale.
Elle indique également un contact supplémentaire avec le bord extérieur de la glissière (en plus du fond de la glissière) : la bille y est plaquée.
Cette dernière force est une force de liaison (interne), due à la contrainte appliquée au mouvement sous forme de trajectoire circulaire.
La force tangentielle peut être soit motrice : la bille est lancée avec une vitesse initiale
par exemple, soit résistante si les frottements sont présent. Sans ces derniers, le mouvement est circulaire uniforme :
).
Remarque :
La résolution est plus aisée avec une approche énergétique qui tient compte uniquement des forces qui travaillent, (donc celles extérieures), et ignore les forces de liaison qui ne travaillent pas. (Chapitre 2)
Exemple : 2. Mouvement d'une bille dans un rail rectiligne horizontal.
Le rail passe par O et tourne à la vitesse angulaire constante Ω autour de l'axe
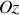. (fig. 6).
Il matérialise la direction radiale des coordonnées polaires.
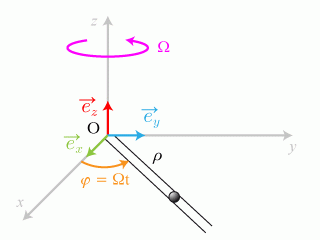
Conseil : Quel mouvement de la bille lorsque le rail tourne ?
Cette visualisation du mouvement permet de déduire les variables du problème : le mouvement a lieu selon
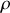et de type accéléré (exponentiel ?) vers l'extrémité du rail entraînant une éjection du rail.
Méthode :
Le contact de la bille avec le rail présente également un intérêt particulier puisque la bille y est "canalisée".
L'analyse en termes de forces mène aux conclusions suivantes :
Le mouvement de la bille, confiné dans le rail, est régie par une inconnue (variable) unique,
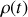. La variable
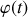est déterminée par la vitesse de rotation du rail, constante sans autres conditions supplémentaires.Du fait du mouvement de rotation du rail (effet d'entraînement), la bille est poussée dans le sens de la rotation et un contact avec le coté arrière (par rapport au mouvement) du rail a lieu, dû à l'inertie de la bille.
D'où une composante de la réaction du rail selon
, perpendiculaire au rail dans le sens du mouvement. (Principe d'action et de réaction)Le poids de la bille est directement compensé par la réaction "au sol" du rail.
La réaction totale du support (au contact) présente donc au moins deux composantes : respectivement selon
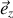et
. Et cela, en l'absence de frottements.
L'application du PFD passe par la formulation générale du vecteur accélération en coordonnées polaires, les plus adaptées pour décrire le mouvement de la bille :
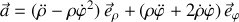
Cette forme permet de traiter plusieurs situations autour du même exercice.
Les accélérations portent, à la masse près, la résultante des forces nécessaires au déplacement, y compris les frottements éventuels.
Deux composantes de l'accélération selon
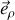(le long de la tige), dont
celle centripète (
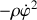) qui n'existe que du fait de la rotation.
Selon
les deux termes n'existent que par la rotation de la tige : d'où une origine inertielle commune, avec une possible accélération angulaire.
Si la vitesse angulaire est constante, la composante horizontale de la force de contact peut être identifiée à
.
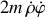En cas de frottements selon les 2 directions du plan, il faut ajouter les expressions des forces de frottement au point de contact.
Ainsi pour une résolution complète du problème, plus de données sont nécessaires.
Complément : Même exercice, autres traitements
Mais d'autres "zooms" sont possibles pour cet exercice.
Il peut être repris ainsi :
En termes de mouvements relatifs (Chapitre 3) :
En considérant le mouvement uniquement selon
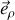, ce qui correspond à la situation d'un observateur qui tournerait avec le rail et mesurerait uniquement le mouvement selon le rail), l'accélération centripète (
) change de signe et devient centrifuge. Selon
, l'accélération
est également dénommée "accélération de Coriolis".Le théorème du moment cinétique, défini par :
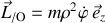peut être appliqué. Si tout frottement est négligé, le poids étant compensé par la réaction du fond du rail, le théorème du moment cinétique s'écrit :
où
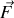est la résultante des forces appliquées, nulle en l'absence de frottement sur le rail. L'accélération selon
nulle. Ceci implique que la pseudo-force de Coriolis (voir le chapitre 3 : mouvements relatifs) n'existe que si la rotation du rail est accélérée.
Une autre conclusion porte sur la conservation du vecteur moment cinétique dont le module :
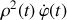est constant. Sans aucune conclusion sur le mouvement selon le rail.
Le moment cinétique n'apporte aucune information sur le mouvement de translation (selon
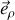), ce qui n'est pas sa fonction.
La richesse de la formulation newtonienne vient de sa forme vectorielle impliquant les forces à l'origine du mouvement : l'équation du mouvement n'est obtenue qu'après avoir fait le tour des variables et des sources de leurs variations.
Aucune description n'est aussi complète ; ce qui en fait un formalisme compliqué.
Toute autre démarche ne peut être que réductrice car simplificatrice mais pouvant constituer une étape d'analyse du problème vers sa solution.
De même la cinématique seule, même en tenant compte des symétries, ne permet pas d'accéder à l'équation du mouvement et donc de résoudre le problème : sans les forces, la cinématique est incomplète.
Une méthode intermédiaire tenant compte de certaines forces "utiles" est de passer par leur énergie, thème du chapitre suivant.
Dans les cas à faibles degrés de libertés (peu de variables ou de dimensions), ce formalisme énergétique permet une description complète du système.
