Le rôle particulier des mouvements rectilignes à vitesse uniforme est illustré par l'exemple suivant :
les mesures comparées de la vitesse
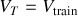(distance entre 2 points, rapportée à la durée du parcours) d'un train à partir
du quai
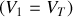et d'une voiture en translation uniforme
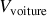sont aisées :
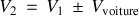selon le sens de déplacement de la voiture.
Si la voiture est en mouvement accéléré ou si une personne court dans le train, la comparaison des mesures va être nettement moins aisée et nécessitera la mise en œuvre de la notion d'accélérations d'inertie. (chapitre 3)
Pour aller du plus simple au plus complexe, le premier élément à ajouter aux trois principes est le suivant.
C'est une 'convention commune à toute la physique' et qui peut être énoncée comme suit :
Fondamental :
Les lois de la physique doivent être indépendantes de l'observateur.
En mécanique, elles sont indépendantes du référentiel : repère + chronomètre.
Cela suppose une invariance de la forme des équations.
Le PFD s'écrira en fonction des forces et de l'accélération mesurées et cela, quel que soit le référentiel où elles seront exprimées, galiléen ou non.
Cette règle est fondamentale pour toute modélisation puisqu'elle nécessite de cerner les conditions expérimentales.
La situation suivante décrit un cas particulier où la règle est toujours vérifiée.
Ainsi le PFD est naturellement invariant lors d'un changement de vecteur-vitesse de type :
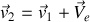où
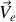est une vitesse d'entraînement uniforme.
En effet,
.
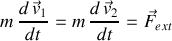Si
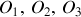... sont les centres des référentiels,
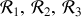,... d'axes fixes dans l'espace et ils se déplaçent à la vitesse uniforme
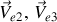... par rapport à
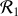, le point matériel
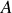peut être repéré par :
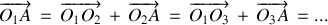
Sa vitesse dans chaque référentiel est déterminée selon ces relations.
Mais son accélération, si elle existe, sera la même partout... et la force à l'origine du mouvement également.
Les référentiels galiléens
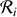sont des référentiels en translation rectiligne uniforme
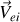, par rapport à l'un d'entre eux, supposé fixe ou lui-même en translation rectiligne uniforme.
Le PFD ou toute loi de la physique, écrit dans un référentiel galiléen, est automatiquement invariant.
Si le référentiel est en mouvement rectiligne ‘non uniforme' ou en rotation (non rectiligne), ou les deux, alors l'application de la règle d'invariance des équations va entraîner quelques ajustements qui seront présentés plus loin. (Chapitre 3).
Néanmoins et en complément des mouvements précédemment décrits, les paragraphes qui suivent vont porter sur la propriété "non rectiligne" d'un mouvement (la rotation) et son influence sur les forces.
Ce type de mouvement a ses contraintes et nécessite la définition d'un nouvel élément cinétique et une analyse spécifique en termes de forces.
