Outils pour décrire un mouvement "non rectiligne"
Lorsque l'action des forces sur le point matériel
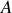est de produire un changement de direction dans le mouvement, ceci entraîne une rotation, fût elle instantanée, du système étudié.
Entre alors en jeu la notion de moment : par rapport à une origine
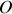, centre de la rotation, le moment de force et moment cinétique (ou vecteur "moment de la quantité de mouvement").
Cette notion s'exprime à l'aide du produit vectoriel de 2 vecteurs.
Pour un point
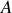en mouvement avec une vitesse
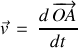et soumis à une force
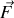, les deux définitions de moment suivantes sont générales :
Définition : Le moment cinétique, un élément cinétique additif
Le moment cinétique est défini par :
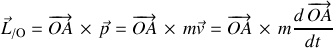
C'est le moment de la quantité de mouvement de la particule de masse
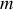, repérée par son rayon vecteur
.
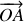Définition : Le moment de force
La grandeur vectorielle
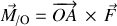est le moment de la force
.
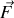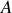est le point d'application de la force et
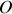, un point distinct qui peut être le centre d'un repère et/ou un point appartenant à un axe de rotation identifié.
La relation entre ces deux moments se déduit, en toute généralité, des définitions de moments ci-dessus et en utilisant le PFD.
Il s'agit du théorème du moment cinétique.
Fondamental : Le théorème du moment cinétique
La variation au cours du temps du moment cinétique évalué par rapport à une origine
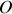est produite par le moment, par rapport à
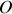, de la résultante des forces :
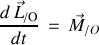
Le point d'application des moments est un choix important.
Le PFD est utilisé : ses conditions d'application sont donc propagées.
Attention : Produit vectoriel, efficacité dans la rotation.
Dans les calculs de moment, les points d'application et la direction des vecteurs ainsi que le centre par rapport auquel est calculé le moment sont fondamentaux.
Ils définissent un bras de levier à l'origine du changement de direction et de la rotation. D'où l'insistante notation en indice :
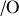synonyme de "par rapport à
".
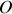En effet et par définition du produit vectoriel, si la force est décomposée selon les directions parallèle et perpendiculaire à
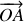le calcul du moment :
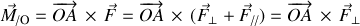
permet d'isoler la composante efficace de la force (
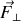) et à l'origine de la rotation.
Et
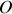est le centre par rapport auquel s'effectue la rotation.
Explication : Bras de levier et projections
Dans ce qui précède, une propriété du module du moment de deux vecteurs
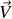et
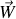selon
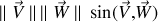a été utilisée.
Hors situation triviale, le module est nul lorsque les deux vecteurs ont même direction.
Il est optimum (ou efficace) lorsque les deux vecteurs sont perpendiculaires.
Il y a deux façons d'optimiser ce module :
projeter la force, comme ci-dessus, et garder l'intégrité de
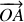ouprojeter
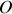sur la direction de la force pour obtenir
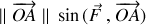: cette expression représente le bras de levier utilisé pour le calcul du moment.
Exemple : Mouvement de rotation
La relation directe entre les 2 moments ci-dessus et le changement de direction peut être "visualisée" au moyen de l'exemple suivant.
Les coordonnées polaires (
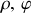) sont utilisées dans le cadre d'une trajectoire plane dans le plan
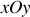et où le point matériel
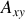de la fig. 2 est repéré par
.
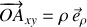La vitesse du point
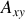peut être notée :
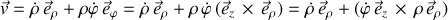
Le moment cinétique s'écrit :
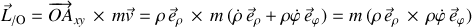
soit :
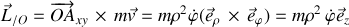
La partie "rectiligne" du mouvement est observée selon
.
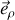En effet, dans un référentiel mobile en rotation avec ce vecteur unitaire, l'observateur ne mesure que ce qui se passe selon cette direction.
La signature de la rotation et du changement de direction est un déplacement selon
.
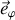Le vecteur moment cinétique ne conserve donc que la composante issue du changement de direction du mouvement.
L'effet du produit vectoriel est donc d'extraire la partie non rectiligne de la vitesse (exprimant donc le changement de direction par rapport à
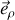et à l'observateur) pour remonter à l'origine de ce changement de direction.
Le moment cinétique est également dénommé "moment angulaire".
Le résultat en est un vecteur perpendiculaire au plan
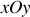, porté par la troisième direction des coordonnées cylindriques et de vecteur unitaire
.
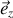Cette direction correspond à celle de l'axe de rotation, notée
.
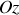Apparaît ainsi le vecteur vitesse ‘rotation' (ou vitesse angulaire) noté
.
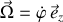Une écriture simplifiée du moment cinétique selon :
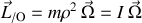
est utile pour décrire directement les rotations des solides.
En résumé, le moment cinétique obtenu est un vecteur porté par l'axe de rotation.
Il ne conserve du mouvement que la rotation : il représente une sorte de "quantité de mouvement de rotation", un moment angulaire.
Autour du vecteur vitesse angulaire, ou rotation
Les notations suivantes ont été adoptées pour leur généralité :
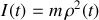représente un moment d'inertie, instantané dans le cas général, du point
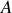en mouvement non rectiligne dans le plan,
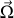, le vecteur vitesse rotation ou vitesse angulaire, porté par l'axe de rotation, (
).
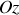Les notations adoptées pour le moment cinétique sont valables pour tout mouvement décrit en coordonnées polaires, comprenant une variation au cours du temps du rayon-vecteur, le long de
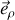mais également un changement de direction dans le plan
.
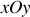Tout déplacement élémentaire
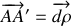est produit par la composition de 2 déplacements élémentaires suivant la relation
.
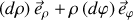La vitesse, dérivée mathématiquement, prend en compte les déplacements élémentaires rapportée à leur durée, supposée infinitésimale.
Elle comprend également deux termes dont le changement de direction.
Ceci permet la séparation de la vitesse selon
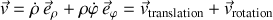
Le terme exprimant la rotation, et le changement de direction, s'écrit :
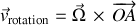
Cette notation est encore mieux adaptée pour un solide en rotation autour d'un axe, ici (
).
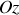En effet chaque point du solide
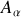, pris séparément, décrit un cercle ‘droit' autour de l'axe de rotation : le solide étant indéformable, le rayon de chaque point est constant et correspond à la distance du point
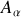à l'axe
.
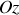Le moment cinétique du point
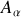s'écrit :
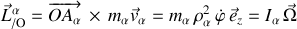
Dans le grain 3, relatif au mouvement des solides, sera démontré le caractère absolu du vecteur-vitesse angulaire : il est commun à tous les points, indépendant de la position de chaque point
.
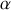Il décrit ainsi la rotation de tout le solide.
Ceci permettra, dans l'écriture du moment cinétique total, l'émergence d'un moment d'inertie pour tout le solide, uniquement associé à l'axe de la rotation décrite.
Complément : Énergie cinétique en coordonnées polaires.
L'énergie cinétique, constituant un élément descriptif du mouvement, sera vue plus en détail au chapitre 2.
Mais pour profiter de la décomposition ci-dessus et pour un mouvement du point matériel
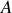exprimé dans les notations précédentes, elle s'écrit :
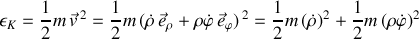
Une additivité en énergie cinétique de deux mouvements apparaît, due à l'orthogonalité des vecteurs de base.
Le premier terme décrit la translation selon
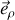et le second est le fruit de la rotation autour de l'axe
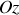, selon
.
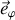D'où la notation simplifiée suivante :
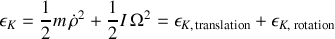
Ces notations et formulations sont orientées, pour leur simplicité, vers la composition des vitesses.
Elles introduisent un référentiel mobile, non galiléen car en rotation autour d'un référentiel fixe : ceci introduit un terme d'entraînement. (chapitre 3)
Leur application aux systèmes de points matériels renforcera leur utilité.
Et l'additivité de l'énergie cinétique, qui s'ensuit, peut servir dans un formalisme énergétique comme celui lagrangien ou canonique.
Le paragraphe suivant précise la difficulté d'exprimer les forces de contact lorsque les mouvements comportent des contraintes de type rotation.
