La même démarche est appliquée pour dériver totalement l'accélération du mouvement.
Directement pour le membre de gauche dans
,
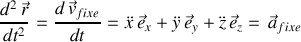
Pour le second membre il faut veiller à extraire toutes les contributions des composantes exprimées dans le référentiel mobile.
Ainsi la dérivée de
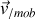est à l'origine de deux termes, dont le premier est :
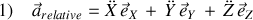
ainsi que 2)
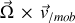qui provient de la dérivation des vecteurs de la base mobile (selon ).
La vitesse du point
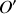contribue directement à l'accélération de ce point, toujours dans
.
Le terme de rotation
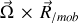est un 'produit' de 2 vecteurs exprimés chacun dans
.
Il est donc la source de
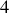contributions mais seuls 3 termes subsistent.
Finalement, dans le référentiel mobile, le détail des différentes contributions est :
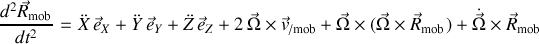
La notation standard qui condense l'ensemble des termes est la suivante :
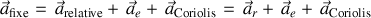
L'accélération d'entraînement se décline en
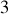termes :
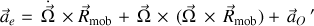
comprenant l'accélération centripète
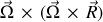et les contributions en accélérations angulaire et du centre
.
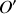Définition :
L'accélération centripète est définie par l'expression :
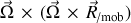
Cette accélération est contenue dans l'accélération d'entraînement.
Elle est perpendiculaire à la vitesse angulaire de rotation et toujours dirigée vers le centre de rotation du mouvement circulaire considéré, comme il sera démontré plus loin.
Définition :
L'accélération de Coriolis est définie par l'expression :
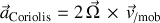
Cette accélération, isolée dans la somme des accélérations, n'existe que si le système étudié est en mouvement avec une vitesse relative non nulle (dans le référentiel mobile).
Par construction, elle est notamment perpendiculaire à la vitesse relative.
Remarque :
L'accélération
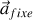mesurée (et évaluée) dans le référentiel fixe galiléen,
, est ainsi exprimée en fonction d'accélérations partielles dont
celle directement mesurée dans le référentiel mobile et
celles d'entraînement exprimées dans l'un ou l'autre des référentiels.
Il est donc essentiel de comprendre l'origine de chaque terme.
Par ailleurs elle remplit les conditions d'application du PFD soit :
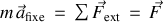
où
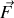est la résultante des forces extérieures qui s'appliquent sur une particule
.
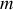