La cinématique a permis d'écrire les éléments cinétiques entre les 2 référentiels, l'un galiléen ("fixe") l'autre non galiléen.
Une composition de mouvements a été mise en évidence, identifiant l'effet et l'origine de chacun et adoptant une notation qui explicite leur apport respectif.
Le PFD étant applicable dans
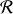, il reste à utiliser la composition des accélérations pour écrire le PFD dans
.
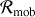Pour cela il faudra veiller à l'invariance de la forme des équations lors du passage du référentiel
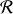à celui
.
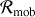Ainsi le PFD dans le référentiel mobile doit s'écrire sous la forme :
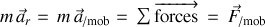
Il reste alors à identifier la résultante des forces dans
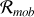, notée
.
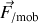Dans
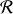, le PFD s'écrit
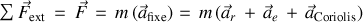
Les accélérations d'entraînement et de Coriolis contribuent à
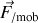en produisant des forces d'inertie, ou pseudo-forces, du même nom.
Il vient que :
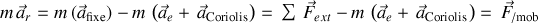
expression qui regroupe toutes les contributions.
La résultante des forces dans le référentiel mobile prend ainsi la forme :
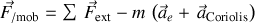
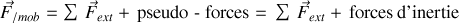
Ces pseudo-forces n'existent que parce que le référentiel mobile non galiléen
est accéléré transformant l'espace de mesure en espace inhomogène et
présente des rotations, l'espace devenant anisotrope.
Ainsi ces deux mouvements sont à l'origine des accélérations d'inertie.
Ils donnent lieu aux ‘pseudo-forces' également dénommées forces d'inertie.
Rappel : L'entraînement, décrit en accélération par
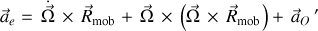
contient
effets d'accélération :
de translation de
et des rotations via les accélérations centripète et angulaire.
Les pseudo-forces d'entraînement expriment une opposition (avec le signe moins), une inertie aux effets de ces entraînements.
.
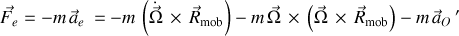incluant la pseudo-force centrifuge.
Quant à l'accélération de Coriolis, elle contribue à une pseudo-force de Coriolis selon :
.
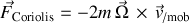qui a les mêmes caractéristiques vectorielles que l'accélération de Coriolis mais de sens opposé.
Remarque : Et les systèmes de coordonnées ?
Tous ces effets dus aux rotations, notamment, apparaissent explicitement dans les expressions des vitesses et accélérations en coordonnées polaires, sous la rotation d'angle
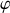autour de l'axe
:
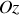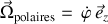
mais également cylindriques (idem) et sphériques
.
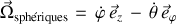Quant à la translation du centre du référentiel mobile, elle se retrouve portée par l'extrémité du rayon-vecteur
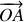, donc la direction
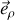ou
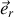selon qu'il s'agisse du système de coordonnées polaires ou sphériques.
Les référentiels associés à ces systèmes de coordonnées sont mobiles et non galiléens.
Pour finir cette partie, il est utile de répondre à la question suivante concernant l'élément cinétique décrivant la rotation :
le moment cinétique et son théorème sont-ils affectés par une description dans un référentiel non galiléen ?
