Problématique et notations

Dans ce chapitre, une réponse aux mêmes questions que précédemment est élaborée mais dans une situation non galiléenne.

Soit :

Lorsque l'espace est inhomogène et/ou anisotrope, que deviennent les éléments cinétiques ainsi que les équations du mouvement ?

Une autre formulation en est la suivante :

Quelles lois régissent les mouvements dans un référentiel non galiléen ? ou

Qu'y mesure t on ?

L'analyse développée dans ce cours décrit le cas le plus général.

Un mouvement incluant une translation accélérée du centre 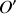du référentiel mobile noté 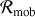et 3 rotations non uniformes de ce dernier ( 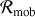) par rapport à un référentiel de centre 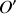mais dont les axes restent parallèles au référentiel considéré comme "fixe", .

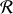Pour cela, les notations suivantes ont été adoptées, les majuscules étant affectées au référentiel mobile. (fig. 10)

Un point matériel 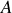est repéré respectivement par :

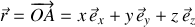
dans le référentiel fixe et sa base, 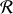, et

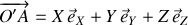
dans celui mobile .

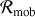La relation entre les deux représentations est :

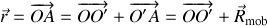
où

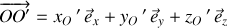
est exprimé dans le repère fixe, .

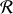Ainsi la translation est décrite par le mouvement du sommet 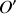et les rotations affectent les vecteurs de la base associée à .

Figure 10 : Représentation des deux repères : "fixe" (minuscules) et mobile (majuscules)

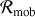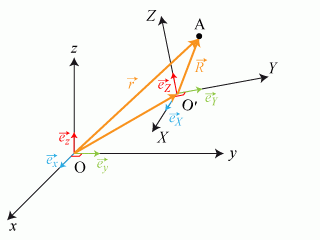
Dans certains cas comme l'étude du système solide, le centre de masse 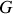remplace avantageusement le centre 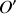du référentiel mobile.

Pour dériver vitesse et accélération, toutes les dépendances, implicites et explicites, seront prises en compte.

Outre la translation du référentiel mobile, représentée par le mouvement de son sommet 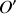, les mouvements de rotation des vecteurs de la base mobile seront décrits par les 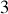rotations possibles dans l'espace.

Le principe fondamental de la dynamique dans le référentiel mobile sera déduit.

Puis dans le but de répondre à des questions récurrentes, l'expression du moment cinétique dans un référentiel non galiléen et l'invariance du théorème du moment cinétique seront explicitées.

Finalement lorsque la rotation propre de la Terre est à l'origine des phénomènes décrits, plusieurs choix de référentiels terrestres seront utilisés pour développer les différents termes et contributions apparaissant dans le PFD.