i Le théorème du moment cinétique
La description d'un mouvement dans un référentiel non galiléen peut comporter l'usage du moment cinétique, outil mathématique associant position et vitesse.
De même le théorème du moment cinétique est exprimé dans un référentiel galiléen fixe de centre
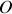selon :
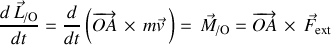
Il met en jeu le moment résultant des forces extérieures lequelle dépend de la position du point d'application des forces dans le cas général et de la position
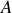du point matériel.
La description du mouvement de rotation dans un référentiel non galiléen passe donc par la connaissance des transformations que subissent ces différents moments.
ii Moment cinétique et référentiel non galiléen
Pour rappel, l'écriture du moment cinétique :
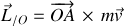passe par la décomposition du vecteur position et la composition des vitesses suivant la notation :
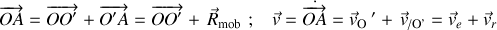
Le moment cinétique dans le référentiel fixe comporte donc les quatre contributions suivantes :
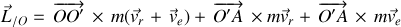
où le moment cinétique "relatif" est reconnaissable (avant-dernier moment).
La relation entre les moments cinétiques exprimés dans le référentiel galiléen et non galiléen s'écrit donc :
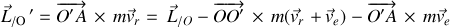
Ou encore :
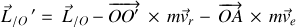
A l'état brut, elle exprime la différence entre les deux moments sous la forme de moments complémentaires.
L'aspect "soustractif" de ces moments rappelle les effets inertiels déjà rencontrés lors de la dérivation du PFD.
iii Le moment de force
Par ailleurs, le moment de la force extérieure s'écrit :
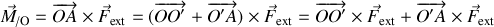
cette relation présente également un terme additif, propre au changement d'origine dans le produit vectoriel.
iv Le théorème du moment cinétique dans le référentiel non galiléen
Dans le référentiel galiléen, le théorème du moment cinétique s'écrit :
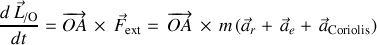
Cette dérivée par rapport au temps tient compte de toutes les variations et mouvements, translation du centre du référentiel mobile et rotations de ses axes.
Cette égalité peut être le point de départ pour une évaluation de la variation temporelle du moment cinétique "relatif" dans le référentiel non galiléen comme pour les compositions de vitesses et accélérations.
Mais dans le référentiel non galiléen, la spécificité de la dérivée temporelle, notée différemment avec (
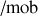), est qu'elle ne tient pas compte du mouvement des vecteurs unitaires ni de l'entraînement de O' (seules les variations des composantes
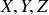sont "visibles").
Fondamental : Théorème du moment cinétique dans un référentiel non galiléen
Cette propriété permet d'écrire la dérivée du moment cinétique "relatif" :
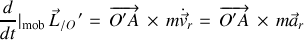
soit :
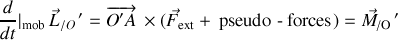
Important :
Ainsi quel que soit le référentiel non galiléen de sommet
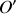, le théorème du moment cinétique est invariant dans sa forme.
Explication :
Ce résultat est prévisible puisque le théorème du moment cinétique est déduit du PFD.
Les règles d'invariance appliquées au PFD sont naturellement propagées.
Les forces d'inertie ont été mises en place pour assurer l'invariance des équations du PFD, elles jouent leur rôle chacune dans un pseudo moment contribuant au moment résultant.
Une vérification-démonstration de ce qui précède peut être proposée à partir de la relation entre les deux moments cinétiques, exprimés dans les deux référentiels moyennant certaines conditions.
Attention :
L'utilisation de la dérivée complète par rapport au temps, appliquée au moment cinétique "relatif" produit la relation intermédiaire suivante :
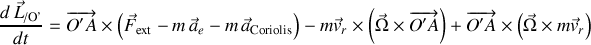
Les termes additifs proviennent de la dérivation des vecteurs unitaires dont les rotations sont ici prises en compte.
Les deux derniers termes ne s'annulent pas toujours.
En effet, l'identité de Jacobi réduit les termes additifs à
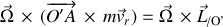
Cette expression n'est nulle que pour une rotation unique : cette condition assure un moment cinétique porté par l'axe de rotation.
Les différents termes proviennent des dérivées de vecteurs unitaires, caractérisant des contributions inexistantes (non perçues) dans le référentiel mobile.
Dans le cas générale, la dérivée temporelle "fixe" ou "complète" se résume en :
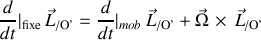
L'équation ci dessus est valide pour tout vecteur soumis à un entraînement de type "rotation".
Cette propriété de dérivation ‘sélective', dans le référentiel mobile, aura un rôle prédominant notamment lors du traitement par le formalisme lagrangien des référentiels non galiléen (grain 2).
Explication :
L'invariance du théorème du moment cinétique peut être obtenue même en utilisant la relation générale entre les moments cinétiques dans les référentiels galiléen et non galiléen :
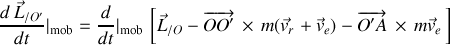
Pour ne conserver ci-dessus que les seules variables du référentiel non galiléen, la dérivée "non galiléenne" du moment cinétique se réduit à l'identité suivante :
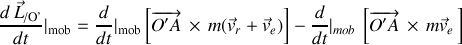
ce qui revient à considérer le moment cinétique dans le référentiel non galiléen seul :
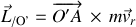
Même en conservant les
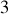contributions, le calcul de la dérivée "effective" en référentiel mobile produit :
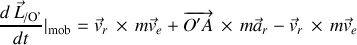
Les termes d'entraînement ne sont pas dérivés puisque leurs variations ne sont pas perçues dans le référentiel mobile.
Il en est de même des termes relevant de mesures propres au référentiel fixe, comme celles du mouvement de
.
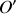Une démonstration, plus complexe, utilisera la formule liant dérivée complète et dérivée mobile permet de retrouver l'invariance du théorème du moment cinétique.
La généralisation à
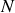corps fera l'objet d'un développement dans le grain 3 mais axé sur le solide.
Dans ce cas, le sommet du référentiel mobile sera associé à un point du solide (translation globale) et les rotations seront celles du solide autour de ses axes propres.
Le rôle particulier du vecteur vitesse angulaire fait apparaître la notion de tenseur d'inertie, en lieu et place de la masse.
Le moment cinétique ne concernant que les rotations, son expression prendra une forme simplifiée autour des trois rotations spatiales (ou rotations d'Euler), simplifiant également l'écriture du théorème du moment cinétique .
Les forces d'inertie, et notamment leur point d'application, nécessitent un traitement particulier.
